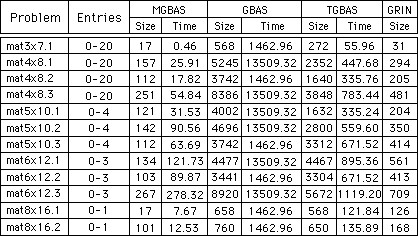
Conventional methods for solving integer programming problems are based on searching algorithms where heuristics such as branch and bound are applied to reduce the search space. Recently, various algebraic IP solvers have been proposed based on the theory of Gröbner bases. The key idea is to encode an IP problem IPA,C into a special ideal associated with the constraint matrix A and the cost (object) function C. An important property of such an encoding is that its Gröbner \ basis corresponds directly to the test set of the IP problem. The main difficulty of these new methods is the size of the Gröbner \ bases generated. In the proposed algorithms, large Gröbner bases are caused by either introducing additional variables or by considering the generic IP problem IPA,C. In a co-operation with researchers from the University of Tsukuba, we have proposed a new algebraic algorithm for solving integer programming problems. based on the Buchburger algorithm. The new algorithm, called the Minimised Geometric Buchburger Algorithm (MGBA), combines various recently developed symbolic IP solvers such as Hosten and Sturmfel's method(GRIN) and Thomas's truncated GBA to achieve a very efficient and general IP solver. We have implemented the system and also carried out experiments to compare this algorithm with others such as the geometric Buchburger algorithm, the truncated geometric Buchburger algorithm and the algorithm in GRIN. These experiments has show that the new algorithm offers significant performance improvements. The experimental results are listed in table 1:
: Experimental Results
This work suggests that it is possible to apply MGBA as a practical IP solver. In particular, we have realised that, for many complex IP problems where there is no efficient solving method available (such as stochastic integer programming), the MGBA provides a new promising solution.
A stochastic integer programming problem is an integer programming problem with uncertain parameters describing optimisation problems with uncertainty. The applications of integer programming range from future productivity in a production problem to a hydro-electric power station to demands at various nodes in a transportation network. Corresponding to the different forms the uncertain parameters (i.e. random vector) may take in the integer programming, the optimisation problems with uncertainty can be divided into two classes: recourse problems and chance constrained problems. The stochastic integer programming also has two models: two-stage stochastic integer programming or stochastic integer programming with recourse and chance constrained integer programming. We consider the two models and give detailed technical approaches as follows.
Stochastic IP, where decisions are made in two stages and the observation of a (vector valued) random variable takes place in between, are called two-stage stochastic IP or stochastic IP with recourse. The two-stage stochastic IP model is specified by the following formulation:
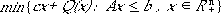
where
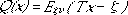
and
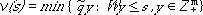
We can interpret this formulation as one which presents a decision with
possible recourse actions, that is, we hope to find an optimal solution
x
that minimises the sum of the original first stage costs cx and the
expected
recourse costs Q(x). The recourse action involves compensating for a
decision x due to the degree of violation of the constraints. For
instance, we make a
production plan in which the clients' demands must be satisfied and the
costs
of production are minimal. In practice it is
very likely -- according to the
production plan and the unforeseen events determining the clients'
demands or
productivity -- that the demands cannot be covered by the production,
which will
require the recourse action to compensate for the ``penalty'' cost. This
shortage has to be bought from the market. The costs due to shortage of
production are actually determined after the observation of the random
data and
are the recourse costs. In the second equations (2) and (3), the
recourse
action ask for an optimal decision y and use Q(x) to represent the
recourse cost by
computing the expectation E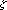
with respect to the random variable
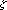. Simply, this model is
designed to find optimal first-stage decisions x in an
optimisation problem under uncertainty where the first-stage decisions
have to be made before knowing the outcome of the random vector
,
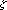and where second-stage decisions y serve to compensate for possible
infeasibilities after having fixed x and observed .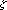
We propose a framework for
solving the two-stage integer programming problems where the
second-stage integer programs are handled efficiently via Gröbner
basis methods from computational algebra. The key idea is solving the
continuous relaxation (i.e. the stochastic program where the integer
requirements in the second stage are dropped) to obtain rough initial
information on the location of the optimal first-stage decisions of
the stochastic integer program. These optimal decisions can be shown
to belong to an explicit countable set, which, under mild assumptions,
is even finite. For every candidate point in the set, we can evaluate
the objective function Q. A candidate with smallest function value
is an optimal solution to the two-stage stochastic integer programming
problem. The key problem of computing function values of Q
(which involves solving the second-stage problem for various
right-hand sides, i.e. s in the constraint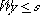 
in equation (3))
is tackled via the minimised geometric Buchburger
algorithm. Since the Gröbner
bases provide a generic representation
of the test sets of a class of integer programming problems
IPA,C
it only needs to be computed once and can be reused when the right
hand
side (involving random variables) changes. This feature provides a
very promising way of saving a lot of repetitive computation for
difference scenarios.
Stochastic IP under probabilistic constraints as a decision model under uncertainty is called chance constrained IP. The model of chance constrained IP, P0 can be described as follows:
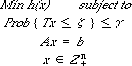
where 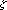is a random variable.
Model P0 has two specialities: (1) the probabilistic constraint is not separable, (2) integer variables are required to model set-up decisions. In currently available techniques for chance constrained programming, no satisfactory solution method exists for models that have integer variables and non-separable chance (probabilistic) constraint arising from non-normal distributions.
Here we propose an algebraic geometry algorithm for solving this class of problems. The key idea is:
