


Next: Developping Generic Symbolic
Up: Developping a Logical
Previous: Background
In the project, we have developed a general
algorithm for modelling IP using first order logic
with arithemic constraints. The whole algorithm will be
present in the full report. Here, we give a brief
summary of the approach.
First we introduce the following forms:
- ge-form: ge(M,S), M or more of S are
true, where M is a integer and S is a set of expressions. The
expressions may be individual logic variable, or linear (in)equalities
involving IP variables, or logic (propositional and predicate) form.
- IP-form: all(P1,P2, ..., Pn), where Pi is a linear (in)equality
constraint involving integer.
It is worth noting that although ge-form is a predicate form, it can
be expanded to a finite expression in the propositional
calculus. There are two extreme cases of the ge-form correspond to
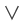 and
and 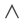 .
.
ge(1,{P1,P2, ..., Pn})
<--->
P1
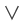 P2
P2
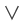 ...PN
...PN
ge(N,{P1,P2, ..., Pn})
<--->
P1
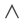 P2
P2
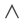 ...PN
...PN
Any statement in the propositional calculus can be put into disjuctive
or conjuctive normal form. Such a form can then be converted the
ge-form (with at most two levels of nesting) using the two special
cases of ge-form above. This procedure can lead to formulations of
enormous size and we therefore follow a different procedure which
results in smaller formulation. So, we can hope to transform a
statement in the input logic form (propositional or predicate form
described in section 3.1) into a ge-form and then transform the
ge-form into an equivalent IP-form.
Our approach for transforming logic form into IP form is just the
transformation of the two forms.
- Description of practical problem in propositional form or predicate form
- original formulation (propositional or predicate form)
--> ge-form
- ge-form --> IP-form
So far, we have developed the algorithm. Using the algorithm,
we have developed and implemented a prototype system in Prolog to
transform a logical specification of multi-objective
decision problem into corresponding integer problem.



Next: Developping Generic Symbolic
Up: Developping a Logical
Previous: Background
www-admin@icot.or.jp
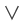 and
and 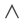 .
.



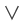 and
and 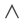 .
.
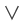 P2
P2
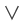 ...PN
...PN
 P2
P2
 ...PN
...PN


