丂
暉堜媊惉丂埾堳
丂
3.4.1.1丂朷傑偟偄HECC
丂
3.4.1.1.1丂HECC偺僯乕僘
丂
丂HECC偑昁梫側暘栰偵偼
乮侾乯儈僋儘側尰徾偲儅僋儘側尰徾偑慻傒崌傢偝傟偰偄傞応崌
丒儈僋儘側尨棟偐傜儅僋儘側尰徾傪夝柧偡傞応崌
丒棎棳寁嶼
乮俀乯儕傾儖僞僀儉惈偑梫媮偝傟傞暘栰
丒婥徾梊應摍
乮俁乯懡偔偺働乕僗偺寁嶼偑昁梫側応崌
丒侾働乕僗偺寁嶼偼偦傟傎偳戝偒偔側偄偑丄
丂寁嶼偺働乕僗悢偑悢愮偐傜悢枩働亅僗偺応崌
偺傛偆側傕偺偑偁傞丅偙傟傪慜採偵偳偺傛偆側僔僗僥儉偑朷傑偟偄偐偵偮偄偰弎傋傞丅
丂
3.4.1.1.2丂恖娫偵偲偭偰巊偄堈偄HECC
丂
寁嶼婡偺儐乕僓偑栤戣夝寛偺偨傔偵寁嶼婡傪巊偆応崌丄儌僨儖乮僾儘僌儔儉乯婰弎偑梕堈側偙偲偑戝愗偱偁傞丅儐乕僓偵偲偭偰丄墘嶼偑懍偄偙偲偑昁梫側傢偗偱偼側偔丄夝偒偨偄栤戣偑懍偔夝偗傞偙偲偑昁梫偁傞丅HECC偱偺儌僨儖乮僾儘僌儔儉乯婰弎偼偳偺傛偆偵偡傞偺偑丄朷傑偟偄偺偐丠
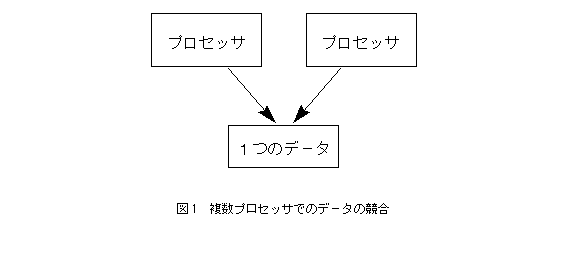
偙偙偱偼丄HECC偼暲楍寁嶼婡偲壖掕偡傞丅尰嵼丄晛捠偵巊傢傟偰偄傞庤懕偒宆尵岅乮Fortran,C摍乯偼僲僀儅儞宆寁嶼婡傪慜採偵偟偰偄傞丅僾儘僌儔儉乮儌僨儖乯偼偳偺僨乕僞傪偳偺傛偆偵壛岺偡傞偐偺庤弴傪寁嶼婡偵巜帵偡傞偙偲偵傛傝峔惉偝傟偰偄傞丅尰嵼偺傾僾儕働乕僔儑儞傕懡偔偺傕偺偼傾儖僑儕僘儉傕僲僀儅儞宆寁嶼婡傪慜採偵偟偰偄傞丅庤懕偒宆尵岅偱偺暲楍僾儘僌儔儉偺嶌惉偼儐乕僓偵偲偭偰晧扴偑戝偒偄丅傑偨丄暲楍寁嶼婡偱偼丄扨撈僾儘僙僢僒偱偼栤戣偲側傜側偄暋悢僾儘僙僢僒娫偺僞僀儈儞僌偺栤戣傕惗偠傞乮恾侾乯丅僞僀儈儞僌偵偐傜傓栤戣偼嵞尰惈偑梕堈偱側偄偙偲偑懡偔丄偙傟偑庤懕偒宆尵岅偱偺暲楍僾儘僌儔儈儞僌偺崲擄偝偺堦場偱偁傞丅偝傜偵丄尰嵼偺暲楍寁嶼婡偼奺寁嶼婡偛偲偵惈擻傪敪婗偝偣傞偨傔偺庤朄偑堎側偭偰偄傞偙偲偑懡偔丄儐乕僓偵偲偭偰丄晧扴偲側偭偰偄傞丅
暲楍寁嶼傪巊偄堈偔偡傞偨傔偵偼丄暲楍寁嶼婡岦偒偺儌僨儖婰弎丒傾儖僑儕僘儉偑偁傞傋偒偱偁傞丅 儐乕僓偵偲偭偰丄庤懕偒宆尵岅偱暲楍僾儘僌儔儉傪彂偔偙偲偼晧壸偑戝偒偔丄偦傟偑壜擻側恖岥偼尷傜傟偰偟傑偆丅暲楍張棟偺儐乕僓傪奼戝偡傞偨傔偺忈奞偵側傞丅儐乕僓偵偲偭偰丄儌僨儖婰弎偲儌僨儖偺曄峏偑梕堈偱丄暲楍惈偺拪弌偑寁嶼婡僔僗僥儉偵偲偭偰梕堈偱偁傞偙偲偑朷傑偟偄丅
 旕庤懕偒宆偱儌僨儖乮僾儘僌儔儉乯傪婰弎偡傞曽朄傕夝寛偺偨傔偺侾偮偺曽嶔偱偁傞丅旕庤懕偒宆尵岅偲偼丄僾儘僌儔儉傪庤懕偒偱偼側偔丄娭悢宆側偄偟偼僆僽僕僃僋僩巜岦揑偵場壥娭學偩偗傪擟堄偺弴彉偱婰弎偡傞偙偲偱偁傞乮恾俀乯丅娭悢宆側偄偟偼僆僽僕僃僋僩巜岦揑側旕庤懕偒宆尵岅偱丄暲楍僾儘僌儔儉乮儌僨儖乯傪婰弎偡傞偙偲偼恖娫偺巚峫偵偁偭偰偍傝丄旕忢偵梕堈偱偁傞丅惂屼宯偱椙偔巊梡偝傟傞僽儘僢僋僟僀傾僌儔儉偑椙偄椺偱偁傞乮恾俁乯丅
旕庤懕偒宆偱儌僨儖乮僾儘僌儔儉乯傪婰弎偡傞曽朄傕夝寛偺偨傔偺侾偮偺曽嶔偱偁傞丅旕庤懕偒宆尵岅偲偼丄僾儘僌儔儉傪庤懕偒偱偼側偔丄娭悢宆側偄偟偼僆僽僕僃僋僩巜岦揑偵場壥娭學偩偗傪擟堄偺弴彉偱婰弎偡傞偙偲偱偁傞乮恾俀乯丅娭悢宆側偄偟偼僆僽僕僃僋僩巜岦揑側旕庤懕偒宆尵岅偱丄暲楍僾儘僌儔儉乮儌僨儖乯傪婰弎偡傞偙偲偼恖娫偺巚峫偵偁偭偰偍傝丄旕忢偵梕堈偱偁傞丅惂屼宯偱椙偔巊梡偝傟傞僽儘僢僋僟僀傾僌儔儉偑椙偄椺偱偁傞乮恾俁乯丅
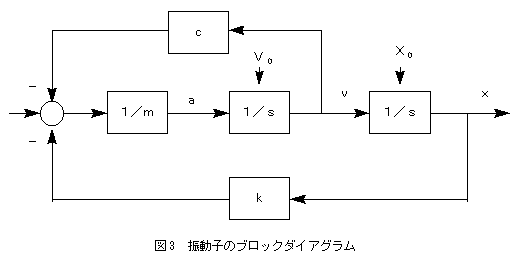 |
庤懕偒宆尵岅偱偼儌僨儖偺寁嶼弴彉傪巊梡幰偑峫椂偟側偗傟偽側傜偢丄彫偝側儌僨儖偱偼梕堈偱偁傞偑丄戝偒側儌僨儖偱偼擄堈搙偑憹偡丅傾僾儕働乕僔儑儞傪奐敪偡傞偲偒偺僱僢僋偲側傞丅
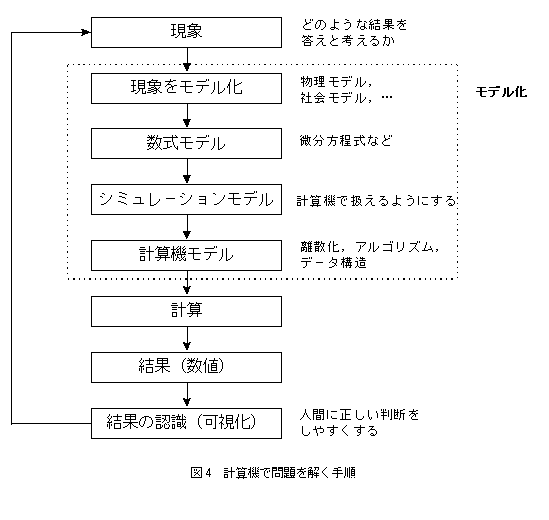
暿妏搙偐傜寁嶼偺庤弴傪峫偊傞丅寁嶼婡偱偺僔儈儏儗乕僔儑儞庤弴乮尰徾偐傜寁嶼寢壥偺擣幆傑偱乯傪峫偊傞偲恾係偺傛偆偵側傞侾乯丅
恾係偱HECC偑桳岠側偺偼丄寁嶼偺晹暘偱偁傝丄寁嶼傪岠壥揑偵恑傔傞偨傔偵偼寁嶼偺慜屻偺嶌嬈偑岠棪揑偵峴傢傟側偗傟偽丄慡懱偲偟偰椙偄寢壥偼摼傜傟側偄丅摿偵丄 HECC偱寁嶼偺晹暘偑崅懍壔偝傟傞偙偲偵傛傝丄寁嶼偺慜屻偺巊偄堈偝偑傑偡傑偡廳梫偵側傞丅 HECC偺惈擻傪廫暘敪婗偝偣傞偨傔偵偼丄寁嶼偩偗偺崅懍壔偩偗偱偼側偔丄寁嶼偺慜屻偺張棟偺崅懍壔偑廳梫偱偁傞丅
寁嶼婡偑崅懍壔偟丄寁嶼庤朄傕崅搙壔偡傞偙偲偵傛傝丄栤戣夝寛偺僼儘乕偺拞偱寁嶼偺愯傔傞斾廳偑抜乆掅壓偟偰偄傞丅帺摦幵偺幵懱嫮搙夝愅乮徴撍夝愅乯偱偼丄寁嶼傛傝傕儊僢僔儏嶌惉偺斾廳偺傎偆偑戝偒偔側偭偰偄傞丅寁嶼偼悢擔偁傟偽廔椆偡傞偑丄儊僢僔儏嶌惉偵偼悢儢寧偑昁梫偵側偭偰偄傞丅偙偺傛偆側晹暘偵傕寁嶼婡僷儚乕傪棙梡偟偰抁弅偡傞偙偲傕廳梫偵側偭偰偄傞丅寁嶼偺崅懍壔偵傛傝丄寁嶼偦偺傕偺傛傝傕丄儌僨儖嶌惉乮儊僢僔儏乯偵斾廳偑堏傞丅崱屻偼丄傑偡傑偡丄栤戣夝寛偺慡懱偺帪娫偑廳梫偵側傝丄栤戣夝寛偺庤弴偺拞偱嵟傕帪娫偺妡偐傞晹暘傪懍偔偡傞偙偲偑廳梫偲側傞乮儌僌儔偨偨偒乯丅偦偺偨傔偵偼丄悢抣揑寁嶼偩偗偱偼側偔丄悢幃張棟丄恖岺抦擻摍偺旕悢抣揑張棟傕慻傒崌傢偣偰丄偍屳偄偺椙偄偲偙傠傪棙梡偟丄栤戣夝寛偺慡懱偺帪娫傪抁弅偡傞偙偲偑廳梫偲側傞
丂
3.4.1.1.3丂暲楍壔偺曽岦
丂
崱屻偺崅惈擻偺寁嶼婡傪峔惉偡傞偵偼暲楍壔偼晄壜寚偱偁傞丅偦偺偨傔丄暲楍壔傪悇恑偡傞偵偼丄尰嵼丄崅壙側暲楍寁嶼婡偺壙奿傪埨偔偡傞昁梫偑偁傞丅 暲楍寁嶼婡傪晛媦偝偣偰丄壙奿傪掅尭偝偣傞偙偲偑廳梫偱偁傞丅偦偺偨傔偵偼暲楍壔偑峴偄堈偄暘栰偐傜丄暲楍壔傪峴偆傋偒偱偁傞丅僷儔儊僩儕僢僋丒僗僞僨傿側偳偼暲楍壔偟傗偡偄暘栰偱偁傞丅尰幚揑偵偼丄慳棻搙偺栤戣偐傜庤傪偮偗傞偙偲傕昁梫偱偁傞丅乮偙傟偼嵶棻搙偺暲楍壔傪斲掕偟偰偄傞偺偱偼側偄丅暲楍張棟傪晛媦偝偣傞偲嵶棻搙偺暲楍壔偑傛傝廳梫偵側傞丅傑偢偼暲楍張棟偺晛媦偲偄偆堄尒偱偁傞丅乯
丂
3.4.1.1.4丂傑偲傔
丂
HECC傪巊梡偡傞偱偁傠偆儐乕僓偑杮幙揑乮捈愙揑乯偵梸偟偄傕偺偼壓婰偺傛偆側傕偺偱偁傞丅
丂丂乮侾乯懍偔惓偟偄寢壥偺摼傜傟傞摴嬶
丂丂乮俀乯栤戣偺張棟夁掱慡懱偑懍偔側傞偙偲
偙傟傪幚尰偡傞偨傔偵偼丄 HECC偺傛偆側懍偄寁嶼婡偲儌僨儖乮僾儘僌儔儉乯婰弎庤朄乮旕庤懕偒宆丄儅僋儘儗儀儖側偳乯偺曄峏偲戝婯柾寁嶼偺慜屻偺張棟偺崅懍壔丒崅搙壔偱偁傞丅慜屻偺張棟偺崅懍壔丒崅搙壔偵偼悢抣揑張棟偩偗偱偼側偔丄旕悢抣張棟偺崅懍壔丒崅搙壔丄擣幆乮偣傑偔偼壜帇壔乯偺崅懍壔丒崅搙壔傕廳梫偱偁傞丅
傑偨丄HECC偑幚尰偡傞偲丄尰嵼丄憐掕偟偰偄偨梡搑埲奜偵傕怴偨側梡搑偑昁偢弌尰偡傞丅偦傟偼夁嫀偺椺偑幚徹偟偰偄傞丅偦偺偨傔偵偼丄 HECC偑懡偔偺恖偵棙梡壜擻偲側傝丄傾僾儕働乕僔儑儞偐傜尒偰桳梡側傕偺偱偁傞偙偲偑廳梫偱偁傞丅
丂
3.4.1.1.5丂晅榐乮嬶懱揑偵梸偟偄婡擻乯
丂
恑揥挊偟偄僨僶僀僗媄弍偱崱屻幚尰偟偰梸偟偄偙偲乮偁傞傋偒巔乯偲俫俹俠暘栰偱梸偟偄媄弍偵偮偄偰弎傋傞丅傑偨丄婰崋張棟偵偮偄偰傕傆傟傞俀乯丅
丂
乮侾乯僨乕僞偺堏摦偺峔憿傪婰弎偡傞庤抜
尰嵼偺寁嶼婡偱戝婯柾側寁嶼乮摿偵丄儔儞僟儉側僨乕僞傪埖偆応崌乯傪峴偭偰偄偰丄嵟戝偺栤戣偼墘嶼偱偼側偔丄僨乕僞偺堏摦偱偁傞丅僲僀儅儞宆寁嶼婡偱偼儊儌儕乕撪偺斣抧傪巜掕偟丄偦偺僨乕僞傪儊儌儕乕偐傜僾儘僙僢僒撪偺儗僕僗僞乕偵堏摦偡傞丅儗僕僗僞乕撪偺僨乕僞摨巑傪墘嶼偟丄寢壥傪暿偺儗僕僗僞乕偵奿擺偟丄偦偺屻丄儗僕僗僞乕偐傜儊儌儕乕偵僨乕僞傪揮憲偡傞偺偑堦斒揑偱偁傞丅墘嶼偼嵟嬤偺僾儘僙僢僒偺崅懍壔偵傛傝丄傎偲傫偳栤戣偲側傜側偄丅儊儌儕乕偲儗僕僗僞乕娫偺揮憲帪娫偑嵟戝偺栤戣偱偁傞丅偙傟偼僾儘僙僢僒偵斾傋偰丄儊儌儕乕偺抶偝偵尨場偑偁傞丅墘嶼傗暘婒惂屼偼姰慡偵儊儌儕乕偲儗僕僗僞乕娫偺揮憲偵塀傟偰偟傑偆応崌傕偁傞丅僾儘僙僢僒偲儊儌儕乕偺懍搙嵎偑偁傞偙偲傪惀擣偡傟偽丄偙偺懍搙嵎傪旔偗傞庤抜傪峫偊傞昁梫偑偁傞丅晛捠丄傛偔峴傢傟傞寁嶼婡傾乕僉僥僋僠儍揑夝寛曽朄偼儊儌儕乕抶墑偺塀暳偱偁傞丅
僜僼僩偺柺偐傜峫偊傞偲尰嵼偺僾儘僌儔儈儞僌娐嫬偵偼僨乕僞偺堏摦偺峔憿傪柧帵揑偵婰弎偡傞庤抜偑側偄丅偦偺偨傔丄昁梫埲忋偵僨乕僞堏摦偺夞悢乮僨乕僞傪帵偡斣抧僨乕僞傕娷傔偰乯偑憹偊偰偟傑偆偙偲偑偁傞丅僨乕僞偺堏摦峔憿傪柧帵揑偵婰弎偱偒傟偽丄寁嶼婡傾乕僉僥僋僠儍揑偵儊儌儕乕抶墑偺塀暳傕梕堈偵側傞丅
偙傟傪幚尰偡傞偵偼僜僼僩揑側奐敪偲偦傟傪巟墖偡傞僴乕僪揑側奐敪偑昁梫偲側傞丅
丂
乮俀乯壜曄僨乕僞僷僗寁嶼婡
慜崁偱弎傋偨僴乕僪揑側奐敪偵棙梡偱偒偦偆側媄弍偑FPGA偱偁傠偆丅FPGA傪棙梡偟偨僔僗僥儉偱偼柦椷懱宯摍傪壜曄偵偡傞尋媶偼栚偵偟偰偄傞偑丄傾僾儕働乕僔儑儞偺惈擻傪忋偘傞偨傔偵偼丄柦椷懱宯偩偗偱偼側偔丄僨乕僞僷僗傪壜曄偵偟偨寁嶼婡偑朷傑傟傞丅壜曄僨乕僞僷僗偲偼昞尰偟偰偄傞偑丄杮摉偵僨乕僞僷僗傪曄峏偟側偄傑偱傕丄僉儍僢僔儏偺惂屼傾儖僑儕僘儉傗僾儕僼僃僢僠偺傾儖僑儕僘儉傪巜掕偱偒傞偩偗偱傕旕忢偵桳岠偱偁傠偆丅
丂
乮俁乯婰崋張棟偵偮偄偰
婰崋張棟偺応崌丄晜摦彫悢揰墘嶼偼旕忢偵彮側偄偺偱丄暥帤張棟偑崅懍偵峴偊傞寁嶼婡偱偁傞偙偲偑昁梫偱偁傞丅嬶懱揑偵偼LISP偺傛偆側尵岅偑崅懍偵張棟偱偒傞寁嶼婡偱偁傞丅婰崋張棟偺1暘栰偱偁傞悢幃張棟偵偍偄偰偼丄儀僋僩儖寁嶼偺傛偆側楢懕揑側儊儌儕乕傾僋僙僗偼彮側偔丄懡偔偺応崌丄儔儞僟儉側儊儌儕乕傾僋僙僗傪峴傢側偗傟偽側傜側偄丅悢幃張棟偱偼儔儞僟儉側儊儌儕乕傾僋僙僗偑崅懍側寁嶼婡偑朷傑偟偄丅
悢幃張棟偵偼傾儖僑儕僘儉傪彂偄偰寁嶼偡傞傕偺偲丄乽岞幃乿傪梡堄偟偰偍偒丄僷僞乕儞擣幆偱峴偆傕偺偑偁傞丅屻幰偺応崌丄僷僞乕儞張棟偑崅懍側寁嶼婡偑昁梫偵側傞丅偙偺揰偼東栿傗壒惡擣幆偲嫟捠側晹暘偑偁傞偺偱偼側偐傠偆偐丅
戝婯柾側壢妛媄弍寁嶼偵栠偭偰峫偊傞偲丄悢抣揑張棟偩偗偱偼廂懇摍偵旕忢偵帪娫偺偐偐傞寁嶼傕悢幃張棟傪忋庤偔慻傒崌傢偡偙偲偵傛傝丄廂懇惈側偳傪戝暆偵夵慞偱偒傞応崌傕偁傞俁乯丄係乯丅
丂
3.4.1.2丂巇慻傒傊偺梫朷
丂
忋偱弎傋偨傛偆偵丄寁嶼婡傪巊偭偰栤戣傪夝偔偲偄偆尨揰偵栠傞偲丄寁嶼偦偺傕偺偩偗偱偼側偔丄儌僨儖壔偺栤戣丄傾儖僑儕僘儉丄寁嶼寢壥傪惓偟偔擣幆偝偣傞媄弍傕廳梫偱偁傞丅婎杮揑側儌僨儕儞僌偵偮偄偰偼丄婇嬈偱偼擄偟偄偨傔丄戝妛傗惌晎偺尋媶強偱偺尋媶偑昁梫偱偁傞丅
擔暷斾妑偱偼懡偔乮傎偲傫偳乯偺傾僾儕働乕僔儑儞偑墷暷惢偱偁傝丄擔杮偼偍姦偄忬嫷偱偁傞丅忋婰偺儌僨儕儞僌偵偮偄偰傕丄暷崙丄墷廈偱偺尋媶偵抶傟傪偲偭偰偄傞丅暷崙偺戝妛偺応崌丄儌僨儖傪奐敪偟丄偦傟傪傾僾儕働乕僔儑儞偵偺偣傞傑偱偺巇帠傪峴偭偰偄傞丅擔杮偱傕偦偙傑偱傗傟傞傛偆側懱惂乮巇帠偺昡壙傑偱娷傔偰乯偑昁梫偱偁傞丅傑偨丄偡傋偰偺暘栰偱墷暷偲懳峈偡傞偙偲偼晄壜擻偱偁傝丄擔杮偑摼堄偲偡傞暘栰偱帺庡惈傪敪婗偡傋偒偱偁傞丅
崱屻偼壓婰偺傛偆側婎慴揑側暘栰偱偺尋媶搳帒偑廳梫偱偁傞丅
丂
丂丒寁嶼婡傪峔惉偡傞慺巕偺婎慴
丂丒婎杮揑側傾乕僉僥僋僠儍
丂丒戝婯柾寁嶼偺偨傔偺傾儖僑儕僘儉乮悢抣寁嶼傪娷傓乯
丂丒徻嵶側尰徾傪昞尰偱偒傞傛偆側儌僨儖壔媄弍乮暔棟揑柺偑戝偒偄乯
丂
傑偨丄僔儈儏儗乕僔儑儞暘栰偱偼僜僼僩偺廳梫惈偑戝偒偔丄偦傟傕棟榑揑側傕偺偩偗偱偼偩傔偱丄幚嵺偵棙梡壜側儗儀儖傑偱偺僜僼僩偺奐敪偑廳梫偱偁傞丅偟偐偟丄擔杮偱偼戝妛摍偱偺僜僼僩偵懳偡傞昡壙偑偝傟偰偄側偄偺偑栤戣偱偁傞丅暷崙偲偺斾妑偵偍偄偰傕嵟戝偺栤戣偱偁傞丅
媄弍奐敪偵偁偨傝丄暷崙桪埵偲側傞擔暷偺嵎偼僜僼僩奐敪偵懳偡傞昡壙偲怴偟偄僜僼僩偵懳偡傞愭庢惈偺桳柍偱偁傠偆丅偙傟偼丄偙傟傑偱擔杮偑墷暷偵捛偄偮偔偙偲偩偗偵廳揰傪偍偄偰偒偨偙偲偺暰奞偱偁傠偆丅
丂
嶲峫暥專
[1] 暉堜媊惉丆HPC傪栚巜偟偰丆忣曬張棟妛夛HPC尋媶夛帒椏93-HPC-46丆pp.1-6丆1993丏
[2] 暉堜丆栰帥丆媣曐揷丆屗愳丆怴悢抣寁嶼丆嫟棫弌斉丆1999丏
[3] Lecture Notes in Computer Science Vol.378 (Ed.)J.H.Davenport, Springer-Verlga 1989. pp.163-171. M.Suzuki, T.Sasaki, M.Sato and Y.Fukui : A Hybrid Algebraic-Numeric System ANS and Its Preliminary Implementation
[4] Journal of INFORMATION PROCESSING, Vol.13, No.4, pp.529-533, 1990. T.Sasaki, Y.Fukui, M.Suzuki and M.Sato: Proposal of a Scheme for LInking Different Computer Languages -from the Viewpoint of Algebraic- Numeric Computation
丂
3.4.2丂旕悢抣寁嶼偺尰忬偐傜尒偨僴僀僄儞僪僐儞僺儏乕僥傿儞僌
媣栧峩堦丂埾堳
丂
壢妛媄弍寁嶼丄摿偵婎慴壢妛偵懏偡傞暘栰偵昁梫側崅惈擻寁嶼傪峴側偆僴僀僄儞僪僐儞僺儏乕僥傿儞僌岦偒偺寁嶼婡偼丄彜嬈揑棙塿傪尒崬傓偙偲偑擄偟偄偨傔丄挿婜揑寁夋偺尦偵岞揑婡娭偑拞怱偲側偭偰媄弍奐敪傪恑傔偰峴偔帠偑廳梫偱偁傞丅
尰嵼傑偱丄儀僋僩儖寁嶼婡偵戙昞偝傟傞儌僲儕僔僢僋側峔憿傪帩偮寁嶼庤朄偑丄壢妛媄弍寁嶼偵偍偗傞崅惈擻寁嶼偺庤朄偲偟偰丄傕偭偲傕桳岠偱偁偭偨丅儀僋僩儖寁嶼婡偼崅惈擻媄弍寁嶼偵昿斏偵弌尰偡傞峴楍寁嶼傪岠棪椙偔幚尰偡傞傾乕僉僥僋僠儍偱偁偭偨偨傔偱偁傞丅
堦曽丄寁嶼婡偺彜嬈棙梡偺暘栰偱偼丄崅惈擻寁嶼偲偼丄僨乕僞儀乕僗僔僗僥儉偵傛傞僆儞儔僀儞僩儔儞僓僋僔儑儞張棟偑廳梫偱偁傝丄嬤擭偱偼僀儞僞乕僱僢僩側偳偺捠怣婎斦惍旛偺偨傔偵丄寁嶼擻椡梫媮偺憹戝偑旘桇揑偵憹戝偟偰偒偨丅僆儞儔僀儞僩儔儞僓僋僔儑儞張棟偼丄壢妛媄弍寁嶼偲偼摦嶌偑慡偔堎側傞傕偺偲峫偊傜傟偰偄傞偑丄幚嵺偵偼丄埲壓偵弎傋傞傛偆偵丄棧嶶宯偺僔儈儏儗乕僞偺摦嶌偲椶帡偡傞揰傕懡偄丅
杮愡偱偼丄戙昞揑側僆儞儔僀儞僩儔儞僓僋僔儑儞張棟儀儞僠儅乕僋偱偁傞TPC-C儀儞僠儅乕僋偵傒傞張棟撪梕傪摿挜偯偗丄偝傜偵丄崅惈擻壢妛媄弍寁嶼偲偺娭學偵偮偄偰専摙傪峴側偆丅
丂
3.4.2.1丂價僕僱僗傾僾儕働乕僔儑儞偲廬棃宆壢妛寁嶼偺憡堘
丂
尰嵼惗嶻偝傟偰偄傞崅惈擻寁嶼婡乮僒乕僶乯偺傎偲傫偳偼丄媄弍宯寁嶼偱偼側偔僨乕僞儀乕僗僔僗僥儉乮DBMS乯偵傛傞僆儞儔僀儞僩儔儞僓僋僔儑儞張棟偵梡偄傜傟偰偄傞丅堦斒偵丄僆儞儔僀儞僩儔儞僓僋僔儑儞張棟偼丄I/O儃僩儖僱僢僋偵傛傝惈擻偑棩懍偝傟丄CPU傾乕僉僥僋僠儍揑偵偼夵慞偺梋抧偑側偄偲峫偊傜傟傗偡偄偑丄廫暘偵惈擻僠儏乕僯儞僌偝傟偨僔僗僥儉丄偦偺拞偱傕僩儔儞僓僋僔儑儞張棟偺儀儞僠儅乕僋應掕傪峴側偆傛偆側娐嫬偱偼丄CPU偺柦椷幚峴懍搙偑惈擻傪寛掕偟偰偄傞丅壢妛媄弍寁嶼偱偼丄儊儌儕偑CPU偵僨乕僞傪嫙媼偡傞僶儞僪暆偱惈擻偑棩懍偝傟傞偑丄僆儞儔僀儞僩儔儞僓僋僔儑儞張棟偱傕摨條偵丄僉儍僢僔儏儈僗僸僢僩偵傛傞CPU偺僷僀僾儔僀儞僗僩乕儖偱張棟惈擻偑棩懍偝傟傞傛偆側儊儌儕僶僂儞僪側張棟偱偁傞丅
懠曽丄壢妛媄弍寁嶼偲偼堎側傝丄晜摦彫悢墘嶼偺斾廳偼彫偝偔丄柦椷偺傎傏偡傋偰偑惍悢宯偺墘嶼偵尷傜傟傞丅
3.4.2.2丂僆儞儔僀儞僩儔儞僓僋僔儑儞張棟偲棧嶶宯僔儈儏儗乕僔儑儞
丂
僆儞儔僀儞僩儔儞僓僋僔儑儞張棟偱偼丄張棟梫媮偼僔僗僥儉奜晹偺抂枛偐傜敪惗偟丄掕傔傜傟偨帪娫乮悢昩乯撪偵張棟寢壥偺墳摎傪曉偡嶌嬈傪孞傝曉偡丅屄乆偺僩儔儞僓僋僔儑儞偼撈棫偟偰張棟偑偱偒傞偑丄僩儔儞僓僋僔儑儞扨埵偱丄埖偆僨乕僞偵懳偟偰偺攔懠惂屼傪昿斏偵峴側偆丅傑偨丄奺乆偺僩儔儞僓僋僔儑儞娫偺暲楍搙傪岦忋偝偣傞偨傔丄慡懱偺攔懠惂屼偼嬌椡峴側傢偢丄埖偆屄乆偺僨乕僞扨埵偵攔懠惂屼傪峴側偆丅僨乕僞儀乕僗僔僗僥儉屌桳偺婎杮摿惈偲偟偰偼丄僔僗僥儉僟僂儞帪偵傕僩儔儞僓僋僔儑儞偼姰慡偵幚峴偝傟偨偐丄傑偭偨偔幚峴偝傟側偐偭偨偐偺偳偪傜偐偱柍偗傟偽側傜側偄乮尨巕惈乯偙偲傗丄慡僩儔儞僓僋僔儑儞偵懳偡傞儘僌傪婰榐偡傞偙偲偑梫媮偝傟傞丅
僆儞儔僀儞僩儔儞僓僋僔儑儞偱偼丄偳偺傛偆側梫媮偑偄偮抂枛偐傜弌偝傟傞偺偐偼丄妋棪揑偵偟偐梌偊傜傟偰偍傜偢丄張棟偺僗働僕儏乕儕儞僌偼丄摦揑偵峴側傢偞傞傪摼側偄丅屻偵弎傋傞戙昞揑側儀儞僠儅乕僋偱偁傞TPC-C儀儞僠儅乕僋偱偼丄奜晹偐傜偺1偮偺僩儔儞僓僋僔儑儞傪張棟偡傞偨傔偵丄僨傿僗僋傾僋僙僗偑昁恵偲側傞丅僨傿僗僋傊偺傾僋僙僗傪尭傜偡偨傔丄僔僗僥儉撪偵偼朿戝側僉儍僢僔儏傪帩偭偰偼偄傞偑丄侾僩儔儞僓僋僔儑儞摉偨傝悢廫夞偺傾僋僙僗偼昁梫偵側傞丅偙偺僨傿僗僋傾僋僙僗儗僀僥儞僔偼丄僜僼僩僂僃傾偵傛傞儅儖僠僗儗僢僨傿儞僌張棟偱塀暳偝傟傞丅偦偺寢壥丄僔僗僥儉撪偺僩儔儞僓僋僔儑儞張棟偺懡廳搙偼丄僾儘僙僢僒偁偨傝100偐傜悢100掱搙偼昁梫偲側傞丅
媄弍寁嶼偵偍偄偰傕丄偙偺傛偆側峔憿傪帩偮寁嶼偲偟偰丄暘嶶旕摨婜偺棧嶶揑僔儈儏儗乕僔儑儞傪峴側偆僔儈儏儗乕僞偑抦傜傟偰偄傞丅
丂
3.4.2.3丂僆儞儔僀儞僩儔儞僓僋僔儑儞儀儞僠儅乕僋乮TPCC乯偵偍偗傞惈擻
丂
僆儞儔僀儞僩儔儞僓僋僔儑儞儀儞僠儅乕僋偺傂偲偮偱偁傞丄TPC-C儀儞僠儅乕僋張棟偵偍偗傞暲楍岠壥傪幚嵺偺儀儞僠儅乕僋寢壥偐傜堷梡偡傞偲丄埲壓偺昞偵傑偲傔傜傟傞丅偙偙偱偼丄斾妑傪梕堈偵偡傞偨傔丄尰忬偱傕偭偲傕崅偄惈擻抣傪帩偪丄偐偮丄摨堦CPU偱摨堦僜僼僩僂僃傾偵傛傞儀儞僠儅乕僋寢壥偑悢懡偔採弌偝傟偰偄傞Intel偺Pentium-III 550MHz CPU傪巊梡偟偨僔僗僥儉偺幚峴寢壥傪堷梡偟偨丅
昞1偲昞2偱CPU偼摨偠偩偑丄OS偲DBMS偑堎側偭偰偄傞偺偱丄憡屳斾妑偼偱偒側偄丅慜敿偺昞偱偼丄CPU悢傪懡偔偟偰偄偭偨帪偺扨堦CPU摉偨傝偺惈擻楎壔丄屻敿偺昞偱偼丄僋儔僗僞峔憿傪梡偄偨応崌偺惈擻楎壔傪抦傞偙偲偑偱偒傞丅
丂
TPMC=僔僗僥儉偑1暘娫偵張棟偟偨僩儔儞僓僋僔儑儞悢丅
昞1丂Pentium乚III 550MHz巊梡偺SMP僔僗僥儉偺TPCC惈擻
| 僔僗僥儉柤 | TPMC | CPUs | TPMC/CPU | OS/DBMS | |
| Compaq |
ProLiant 8500-550-4P |
26,686 | 4 | 6,671 | MS SQL-EE7.0/NT4.0 |
| HP |
NetServer LH 6000 |
33,136 | 6 | 5,522 | MS SQL-EE7.0/NT4.0 |
| Compaq |
ProLiant 8500-550-8P |
40,697 | 8 | 5,087 | MS SQL-EE7.0/NT4.0 |
昞2丂Pentium乚III 550MHz巊梡偺SMP/僋儔僗僞僔僗僥儉偺TPCC惈擻
| 僔僗僥儉柤 | TPMC | CPUs | TPMC/CPU | OS/DBMS | 僋儔僗僞丠 | |
| Unisys |
e-@ction ES5085R Ent |
48,768 | 8 | 6,096 | MS SQL2000/Win2000 | SMP |
| Compaq |
ProLiant 8500-64P |
152,208 | 64 | 2,378 | MS SQL2000/Win2000 | 僋儔僗僞 |
| Compaq |
ProLiant 8500-96P |
227,079 | 96 | 2,365 | MS SQL2000/Win2000 | 僋儔僗僞 |
丂
偙偺昞偐傜丄CPU悢偑憹壛偡傞偲丄僔僗僥儉惈擻偼岦忋偡傞偑丄SMP峔憿偱偁偭偰傕扨堦CPU摉偨傝偺惈擻偼掅壓偟偰偄傞偙偲偑暘偐傞丅偙偺惈擻掅壓偼丄暋悢偺CPU娫偱偺攔懠惂屼偺懡敪偵傛傞僶僗僩儔僼傿僢僋偺憹壛偵傛傝愢柧偝傟丄暯嬒儊儌儕傾僋僙僗儗僀僥儞僔偺憹戝偵傛傞暯嬒柦椷幚峴帪娫乮CPI: Clock Per Instruction乯偺憹壛偑庡側梫場偱偁傞丅
儊儌儕傾僋僙僗儗僀僥儞僔偑憹戝偟偨寢壥丄僉儍僢僔儏儈僗僸僢僩偵傛傞僷僀僾儔僀儞僗僩乕儖偵傛傝丄僗乕僷乕僗僇儔峔憿偺CPU偱傕丄CPI乮暯嬒柦椷幚峴僋儘僢僋悢丗Clock Per丂Instruction乯偼1傪愗傞偙偲偼弌棃側偄丅忋婰偺儀儞僠儅乕僋幚峴帪偵偼丄悇掕偱CPI偼2.5乚3.5偵払偟偰偍傝丄CPU偺壱摥帪娫偺6妱埲忋偼丄儊儌儕懸偪偵傛傞僀儞僞乕儘僢僋忬懺偵偁傞丅
TPCC儀儞僠儅乕僋僾儘僌儔儉偱偼丄奺抂枛偐傜敪峴偝傟傞僩儔儞僓僋僔儑儞偺90%偼丄偁傜偐偠傔寛傔傜傟偨僨乕僞儀乕僗偵傾僋僙僗偡傞傛偆嬊強壔偝傟偰偄傞偨傔丄僩儔儞僓僋僔儑儞偺嬊強惈偼斾妑揑崅偄丅偦偺寢壥丄僋儔僗僞峔憿偵傛傞惈擻岦忋傪尒崬傓偙偲偑偱偒傞偑丄SMP偺応崌偺惈擻偵斾傋1CPU偁偨傝丄栺1/3掱搙偺惈擻偟偐摼傜傟偢丄慳寢崌僔僗僥儉偵偡傞偨傔偺僆乕僶僿僢僪偑戝偒偄偙偲偑暘偐傞丅偟偐偟丄偙偺嬊強惈傪惗偐偡偨傔偵偼丄僨乕僞偺攝抲丄僗儗僢僪偺攝抲偑擄偟偔丄偙偺攝抲擛壗偵傛傝惈擻偑戝偒偔嵍塃偝傟傞偨傔丄SMP峔憿偱偺僔僗僥儉惈擻偵斾傋尰幚偺惈擻傪岦忋偝偣傞偨傔偺庤娫偑嬌傔偰戝偒偄丅
丂
3.4.2.4丂僆儞儔僀儞僩儔儞僓僋僔儑儞偲戝婯柾壢妛媄弍寁嶼偺憡堘
丂
TPC-C儀儞僠儅乕僋偺懠偺媄弍寁嶼宯儀儞僠儅乕僋偲偼堎側傞摿挜偲偟偰丄寁嶼擻椡偺憹戝偑幚峴懍搙偺抁弅偱偼側偔丄張棟検偺憹戝偵岦偗傜傟偰偄傞帠偑偁偘傜傟傞丅尰忬偺悢愮攞偺墘嶼擻椡傪栚巜偡崅惈擻媄弍寁嶼偵偍偄偰傕丄寁嶼帪娫偺抁弅偩偗偱偼側偔丄惓妋側寢壥傪摼傞偨傔偵寁嶼婯柾偺憹戝偵岦偐偆偲峫偊傞偺偼帺慠偱偁傞丅
 |
丂
嬊強惈偺岦忋偲儗僀僥儞僔偺塀暳偼攚斀偺娭學偱偁傝丄僉儍僢僔儏偺惈擻傪婜懸偡傞尷傝丄嵟揔側懡廳搙偼傾僾儕働乕僔儑儞枅偵堎側傞偨傔丄柧妋側僞乕僎僢僩傾僾儕働乕僔儑儞傪壖掕偟側偄偲丄奺僴乕僪僂僃傾僷儔儊乕僞偺愝掕偼晄壜擻偱偁傞丅
僆儞儔僀儞僩儔儞僓僋僔儑儞偱偼丄抂枛偐傜偺梫媮偵傛傝張棟偑奐巒偝傟傞偑丄僩儔儞僓僋僔儑儞梫媮偼摑寁揑暘晍偑梌偊傜傟偰偍傝丄愭峴偟偰幚峴傪奐巒偡傞偙偲偑弌棃側偄丅
傑偨丄堦偮偺僩儔儞僓僋僔儑儞傪幚峴偡傞嵺偺儊儌儕傾僋僙僗傕丄旕斀暅揑偱丄摑寁揑偵偟偐怳傞晳偄傪抦傞曽朄偑柍偄偺偱僾儕僼僃僢僠偼崲擄偱偁傞丅懠曽丄峴楍梫慺傪偡傋偰傾僋僙僗偡傞傛偆側峴楍墘嶼偲偼堎側傝丄儊儌儕傾僋僙僗偺嬊強惈偼偁傞掱搙妋曐偱偒傞丅廬偭偰丄僉儍僢僔儏儊儌儕偵傛傞庡婰壇傾僋僙僗偺嶍尭偼壜擻偱丄尰嵼偺悢MB偺僉儍僢僔儏儊儌儕偱偺儈僗僸僢僩棪偼0.5%慜屻偱偁傞丅僉儍僢僔儏僒僀僘偺憹戝偲偲傕偵儈僗僸僢僩棪偼慟尭偡傞偑丄偦偺尭彮棪偼偁傑傝戝偒偔側偄丅
丂
3.4.2.5丂挻崅惈擻寁嶼婡峔抸偵岦偗偰偺壽戣
丂
僆儞儔僀儞僩儔儞僓僋僔儑儞張棟傪旕悢抣寁嶼偺戙昞椺偲偟偰峫偊傞偲丄尰忬偺壢妛媄弍寁嶼庤朄偲偼帡偨丄偁傞偄偼堎側偭偨尷奅偑暘偐傞丅
丒慡懱偺摦嶌偑儌僲儕僔僢僋峔憿偱偼側偔丄慳棻搙側偑傜偐側傝偺暘嶶張棟偑峴傢傟偰偄傞寢壥丄張棟偼慡懱偲偟偰偼摨婜揑偵峴傢傟偰偍傜偢丄嫞崌偡傞僨乕僞傊偺傾僋僙僗傪挷掆偡傞偨傔偺僆乕僶僿僢僪偑戝偒偄丅
丒僾儕僼僃僢僠偵傛傞儗僀僥儞僔塀暳偼偱偒偢丄儅儖僠僗儗僨傿儞僌偱偺塀暳傪庢傜偞傞傪摼側偄丅尦偺僾儘僌儔儉偵懡偔偺暲楍搙偑娷傑傟偰偄偨偲偟偰傕丄暋悢CPU偵暋悢偺斾妑揑撈棫側僗儗僢僪傪妱傝摉偰傞偩偗偺暲楍搙傪拪弌偡傞偙偲偑擄偟偄丅
丒奜晹偲偺傗傝庢傝傪婎杮偲偟偰偄傞偨傔丄幚帪娫忋偺惂栺偑壛傢傞丅
丒僋儔僗僞峔憿傪庢傞帠偱丄愨懳揑側惈擻岦忋傪恾傞帠偑弌棃傞偑丄惈擻傪摼傞偨傔偺庤娫偑奿抜偵戝偒偔側傞丅
丂
偙傟傜偺帠偐傜丄崅惈擻媄弍寁嶼偵偍偄偰傕丄戝婯柾側暘嶶僔僗僥儉傪嶌惉偡傞偨傔偺僜僼僩僂僃傾婎斦偺惍旛偑昁恵偱偁傞偙偲偑暘偐傞丅
尰嵼傑偱丄崅惈擻暲楍寁嶼婡僔僗僥儉傪峔抸偡傞丄戝妛娫偁傞偄偼丄崙壠僾儘僕僃僋僩偑擔杮偱傕幚巤偝傟偰偒偨丅偦傟傜偼丄CPU悢偑悢昐戜偺婯柾偱偼偁偭偨偑丄僴乕僪僂僃傾庡摫宆偱嶌惉偝傟偨帠偑懡偔丄僜僼僩僂僃傾嶌惉偺抜奒偱栤戣傪惗偠偨丅僜僼僩僂僃傾偑傢偺棫応偐傜偼丄懚嵼偟側偄戝婯柾僴乕僪僂僃傾岦偗偺僜僼僩僂僃傾奐敪偼晄壜擻偱偁傞偲偄偆尒曽傕偁傞丅偟偐偟丄栚昗偲偡傞偙偲偼丄崅惈擻寁嶼傪昁梫偲偡傞傾僾儕働乕僔儑儞偵懳偟丄梫媮偵尒崌偆崅惈擻僔僗僥儉傪採嫙偡傞偙偲偱偁傞丅斈梡寁嶼婡傪栚昗偲偡傞偙偲偼丄壗偺偲傝偊傕側偄寁嶼婡傪嶌傞偙偲偵摍偟偄丅廬偭偰丄崅惈擻暲楍寁嶼婡僔僗僥儉峔抸偺嵟弶偺壽戣偼丄崅惈擻寁嶼婡傪昁梫偲偡傞傾僾儕働乕僔儑儞傪掕傔丄偦偺傾僾儕働乕僔儑儞偵懳偟昁梫偲偝傟傞僔僗僥儉偺愝寁傪巒傔傞偲尵偆庤弴偱側偗傟偽側傜側偄丅
暷崙偺ASCI寁夋偱偼丄孯帠栚揑偺妀暫婍僔儈儏儗乕僔儑儞偑偙偺傛偆側傾僾儕働乕僔儑儞偲偟偰昅摢偵忋偘傜傟偰偄傞丅傂偲偮偱傕惉岟椺傪嶌惉偡傞偙偲偵傛傝丄偦偺僔僗僥儉惈擻偵懳偟枺椡傪姶偠傞尋媶幰傪堷偒晅偗丄廃曈偵墳梡傪峀偘偰備偔偲尵偆愴棯偲峫偊傜傟傞丅
擔杮偵偍偄偰丄傾僾儕働乕僔儑儞庡摫宆偺僔僗僥儉奐敪傪恑傔傞偨傔丄僜僼僩僂僃傾偲僴乕僪僂僃傾偺嫤挷奐敪偵揔偟偨傾僾儕働乕僔儑儞偺慖掕偑崅惈擻寁嶼婡僔僗僥儉嶌惉傊偺嵟弶偺壽戣偩偲峫偊傞丅
丂
墶愳嶰捗晇丂埾堳
丂
3.4.3.1丂偼偠傔偵
丂
1992擭儕僆僨僕儍僱僀儘偱奐嵜偝傟偨抧媴僒儈僢僩乮UNCED乯偵偍偄偰丄壏幒岠壥僈僗攔弌偺塭嬁傪傛傝惓妋偵攃埇偡傞偨傔偺婥岓曄摦偵娭偡傞崙嵺楢崌榞慻忦栺乮UNFCCC丗United Nations Framework Convention on Climate Change乯偑彁柤偝傟偨丄偙偺摦偒偼丄1990擭偵婥岓曄摦偵娭偡傞惌晎娫僷僱儖乮IPCC丗International Panel on Climate Change乯偑敪昞偟偨戞堦師昡壙曬崘彂偑宊婡偲側偭偰偄傞丅1995擭偺戞擇師昡壙曬崘彂偱偼丄乽拞埵偺僔僫儕僆傪梡偄傟偽丄100擭屻偵偼抧媴慡懱暯嬒婥壏偑俀亷忋徃偟丄暯嬒奀柺悈埵偼栺50cm忋徃偡傞乿偲偄偆徴寕揑側撪梕偑弎傋傜傟偰偍傝丄恖椶偺幮夛宱嵪妶摦偵偍偄偰敪惗偡傞壏幒岠壥僈僗偑抧媴娐嫬偵懡戝側塭嬁傪梌偊傞偙偲傪寈崘偟偰偄傞丅UNFCCC偺栚揑傪嬶懱壔偡傞偨傔偵奐嵜偝傟偨壏抔壔杊巭嫗搒夛媍乮COP3丗The Third Conference on the Parties乯偱偼丄2008擭偐傜2012擭傑偱偺娫偵俇庬椶偺壏幒岠壥僈僗偺慡懱攔弌検傪丄1990擭斾偱彮側偔偲傕俆亾嶍尭偡傞偲偄偆栚昗偵摨堄偟偰偍傝丄壏幒岠壥僈僗偺攔弌梷惂偵傛傞幚幙揑側宱嵪妶摦傊偺塭嬁偑寽擮偝傟傞丅抧媴壏抔壔偺塭嬁傪傛傝徻偟偔攃埇偡傞偨傔偵傕丄抧媴婯柾偺悢抣儌僨儖偵傛傞悢抣僔儈儏儗乕僔儑儞偺廳梫惈偑擣幆偝傟偰偍傝丄偙偺暘栰偺尋媶奐敪偺恑揥偑朷傑傟偰偄傞丅抧媴壏抔壔梊應偺嵟嬤偺榖戣偼丄暥專乵1乶丄乵2乶偵徻偟偄丅
堦曽丄悽奅奺抧偱敪惗偡傞堎忢婥徾偵偮偄偰傕夝柧偝傟傞偙偲偑婜懸偝傟偰偍傝丄摿偵僄儖僯乕僯儑尰徾偲偺娭楢惈偵偮偄偰娭怱偑崅偄乵3乶丄乵4乶丅堎忢婥徾偼丄幮夛宱嵪妶摦偵塭嬁傪梌偊傞偽偐傝偱側偔丄峖悈傗擬攇偵傛傞恖揑旐奞傕戝偒偄丅偙偺傛偆側尰徾偵懳偟偰傕悢抣儌僨儖偵傛傞梊應偼廳梫偝傪憹偟偰偒偰偄傞丅1992擭偺僽儔僕儖杒搶晹偵弌偝傟偨僄儖僯乕僯儑尰徾偵傛傞姳偽偮梊曬偵傛偭偰丄姳偽偮偵嫮偄嶌暔偺慖戰偑側偝傟廂妌傪堐帩偟偨偲偄偆椺偑曬崘偝傟偰偍傝丄偙傟偼悢抣儌僨儖乮悢抣僔儈儏儗乕僔儑儞乯偵傛傞堎忢婥徾梊應偑桳岠偱偁傞偙偲傪帵偟偰偄傞丅
偙偙悢擭丄抧媴娐嫬曄摦偵娭偡傞尋媶偑拲栚偝傟偰偄傞攚宨偵偼丄抧媴壏抔壔梊應傗堎忢婥徾夝柧偑丄偁傞掱搙悢抣僔儈儏儗乕僔儑儞偵傛偭偰壜擻偱偁傞偲峫偊傜傟偰偄傞偐傜偱偁傠偆丅偟偐偟丄抧媴婯柾偺尰徾偼丄帪娫揑丄嬻娫揑偵傕僗働乕儖偺嬌抂偵堎側傞尰徾偑暋嶨偵棈傒崌偭偰惗偠偰偍傝丄偙傟傜偺暋嶨側尰徾偺儊僇僯僘儉夝柧偼旕忢偵崲擄偱偁傞丅傑偨丄婥徾尰徾偼杮幙揑偵僇僆僗偺惈幙傪傕偭偰偍傝丄弶婜抣埶懚惈偑戝偒偄偨傔丄挿婜梊曬偵偼杮幙揑偵尷奅偑偁傞丅偡側傢偪丄乽僶僞僼儔僀岠壥乿偲屇偽傟傞椺偊乮僽儔僕儖偱堦塇偺挶偑塇偽偨偗偽僥僉僒僗偱僩儖僱乕僪偑惗偠傞偙偲偑偁傞乯偳偍傝丄婥徾尰徾偼偁傞応強偺偪傚偭偲偟偨嬻婥偺棳傟偺堘偄偑墦偔棧傟偨婥徾尰徾偵塭嬁傪梌偊偆傞惈幙傪帩偭偰偍傝丄悢抣僔儈儏儗乕僔儑儞偵偍偗傞弶婜抣乮懡偔偼娤應抧偐傜偺悇掕抣乯偺梌偊曽偵傛偭偰偼挿婜梊曬偺寢壥偑戝偒偔堎側偭偰偟傑偆丅
偟偐偟丄婥徾傗婥岓偵娭偡傞悢抣僔儈儏儗乕僔儑儞偑偙偺傛偆側惈幙傪撪曪偟偰偄偨偲偟偰傕丄幚尡偱偼尰徾偺嵞尰偑嬌傔偰崲擄偱偁傞偟丄傑偨棟榑揑夝愅偑晄壜擻偱偁傞偨傔丄悢抣僔儈儏儗乕僔儑儞偑桞堦偺夝愅曽朄偲塢偊傞丅悢抣僔儈儏儗乕僔儑儞偺惛搙傪岦忋偝偣傞偨傔偵偼丄棧嶶壔嬻娫偺夝憸搙傪崅偔偡傞昁梫偑偁傞偑丄尰嵼偺僗乕僷乕僐儞僺儏乕僞偵偍偄偰偝偊丄偦偺擻椡偑廫暘偱側偄丅21悽婭偵岦偗偰丄僴乕僪僂僃傾惈擻偺嫮壔偽偐傝偐丄岠棪傛偄僜僼僩僂僃傾奐敪娐嫬側偳峀斖埻偺僴僀僄儞僪僐儞僺儏乕僥傿儞僌媄弍偺廳梫惈偼尵偆傑偱傕側偄丅
丂
3.4.3.2丂婥徾丄婥岓僔儈儏儗乕僔儑儞偵娭偡傞暷崙偺奐敪忬嫷
丂
暷崙偵偍偄偰傕丄戝婥丄奀梞儌僨儖偵娭偡傞尋媶偑恑傔傜傟偰偄傞丅IT俀僀僯僔傾僠僽偵娭偡傞Bluebook2000偵偼丄戝婥丄奀梞儌僨儖偵娭偡傞尋媶奐敪偲偟偰丄
丒NOAA偵傛傞暘嶶庡婰壇宆暲楍寁嶼婡岦偗奀梞戝弞娐僔儈儏儗乕僔儑儞梡僾儘僌儔儉MOM3乮Modular Ocean Model, version 3乯偺奐敪
丒抧媴棳懱椡妛儌僨儖傪暲楍壔偡傞偨傔偵NOAA / FSL偑奐敪偟偰偄傞婥徾儌僨儕儞僌梡僗働乕儔僽儖僣乕儖SMS乮Scalable Modeling System乯偺奐敪
丒婥徾丄奀梞尋媶偺僐儈儏僯僥傿偱峀偔棙梡偝傟偰偄傞僨乕僞昗弨僼僅乕儅僢僩netCDF偵偮偄偰丄NOAA / GFDL偲LBNL偑峴偭偰偄傞暲楍I/O婡擻偺尋媶
丒NOAA / NCEP偵傛傞暲楍寁嶼婡岦偗偺婥徾梊應儌僨儖偺奐敪
丒NOAA / FSL偑峴偭偰偄傞旘峴婡偵塭嬁傪梌偊傞婥徾偺梊應儌僨儖RCU-2偺奐敪
丒NOAA / NCEP偵傛傞僴儕働乕儞梊應
丒幚帪娫婥徾梊應
偵偮偄偰偺婰弎偑偁傞偑丄徻偟偄撪梕偑彂偐傟偰偄側偄丅偙偙偱偼丄IT俀僀僯僔傾僠僽偺堦晹偱偁傞DOE偺SSI乮Scientific Simulation Initiative乯偺僷儞僼儗僢僩偵増偭偰丄DOE偑幚巤偟偰偄傞婥徾丄婥岓僔儈儏儗乕僔儑儞偵偮偄偰奣娤偟偰傒傞丅
摉慠偺帠側偑傜丄抧媴娐嫬曄摦偺梊應傪峴偆偙偲偼嬞媫傪梫偡傞偲偺棫応偱偁傝丄幙揑偵傕検揑偵傕怣棅偺偁傞梊應偑梫媮偝傟偰偄傞丅偙偺偨傔丄埲壓偵帵偡傛偆側戝婥丄奀梞丄奀昘堟偍傛傃抧昞柺傪峫椂偟偨夝憸搙偺崅偄抧媴婥岓儌僨儖偺奐敪偑栚昗偲側偭偰偄傞丅
嘆怣棅搙偺崅偄梊應偑壜擻側儌僨儖
儌僨儖偵娷傑傟傞暔棟揑僾儘僙僗丄壔妛揑僾儘僙僗媦傃惗暔妛揑僾儘僙僗偼丄廫暘棟夝偑恑傫偱偄傞偙偲偑忦審偱丄尰嵼媦傃夁嫀偺婥岓僨乕僞偲偺斾妑偵傛偭偰丄儌僨儖偺懨摉惈偑廫暘専徹偝傟偰偄傞昁梫偑偁傞丅
嘇掕検揑偵昡壙壜擻側儌僨儖
婥岓曄摦偺梊應抣偼丄僇僆僗揑曄摦偵婎偯偔晄妋幚偝傪廤崌乮傾儞僒儞僽儖乯暯嬒偵傛偭偰昡壙偱偒丄彨棃偺宱嵪惉挿梊應偲偦傟偵婲場偡傞擇巁壔扽慺傗懠偺壔妛暔幙偺曻弌梊應偑昡壙壜擻側儌僨儖偑昁梫偱偁傞丅
嘊夝憸搙偺崅偄嬊強堟儌僨儖
丂尰忬儌僨儖偱偼夝憸搙偑掅偔丄偦偺梊應抣偼抧堟揑丄抧宍丄搚忞丄怉惗丄岺嬈抧堟側偳偺梫場偱戝偒偔曄傢偭偰偟傑偆丅尰嵼偺戝婥儌僨儖偱偼悈暯曽岦300km奿巕媦傃墧捈曽岦20憌偺奿巕丄奀梞儌僨儖偱偼悈暯曽岦100-200km奿巕媦傃墧捈曽岦30-40憌偑梡偄傜傟偰偄傞偑丄嵶偐偄寁嶼奿巕娫妘偑庢傟傞偐偳偆偐偼丄嬊強揑婥岓曄摦梊應傪惛搙椙偔峴偆忋偱廳梫偱偁傞丅尰嵼偺儌僨儖偱偼丄100擭偺婥岓悢抣僔儈儏儗乕僔儑儞傪峴偆偺偵嵟怴偺僗乕僷乕僐儞僺儏乕僞偱傕侾儢寧偼昁梫偱偁傞丅偙偺奿巕娫妘傪尰嵼偺10暘偺侾偲側傞30km偵偡傞偺偑挿婜揑栚昗偱偁傞丅
丂
僗乕僷乕僐儞僺儏乕僞偵懳偡傞梫媮惈擻偵偮偄偰偼丄乽尰嵼偺儌僨儖偱崅偄夝憸搙傪払惉偟傛偆偲偡傞偲丄寁嶼婡偼尰嵼偺彮側偔偲傕100攞偑昁梫偱偁傞丅傑偨丄尰嵼偺儌僨儖偵戝婥偺壔妛曄壔媦傃奀梞偺惗壔妛曄壔摍偺僾儘僙僗偺捛壛傪峴偆偨傔偵偼丄偝傜偵俆攞埲忋偺擻椡偑昁梫偱偁傞丅偝傜偵悈暯曽岦偺奿巕悢傪俀攞偵偟丄偦傟偵墳偠偰墧捈曽岦偺奿巕傪憹壛偝偣傞偨傔偵偼丄悢10攞偺擻椡偑昁梫偱偁傞丅寢壥偲偟偰丄侾儁僞僼儘僢僾僗埲忋偺寁嶼婡偑昁梫偱偁傞偲梊應偝傟傞偑丄偁偲俆擭娫偱偼払惉晄壜擻偲巚傢傟傞丅乿偲弎傋傜傟偰偄傞
僴乕僪僂僃傾偩偗偱偼側偔僜僼僩僂僃傾偺恑揥傕昁梫偲偟偰偍傝丄偦偺応崌偵偼丄墳梡壢妛幰偲寁嶼婡壢妛幰偺嫤椡偑廳梫偱偁傞偲偟偰偄傞丅埲壓偺撪梕偑尋媶偡傋偒壽戣偲偟偰儕僗僩傾僢僾偝傟偰偄傞丅
丒儅僀僋儘僾儘僙僢僒偺岠棪傪俁侽亾偐傜俆侽亾偵偁偘傞僾儘僌儔儈儞僌庤朄
丒儌僨儖曽掱幃偵懳偡傞寁嶼偑娙扨偲側傞掕幃壔
丒暲楍寁嶼婡忋偺婥岓儌僨儖偵摿壔偟偨悢抣夝朄
丒崅搙側僐儞僷僀儔
丒崅搙側悢妛儔僀僽儔儕偲捠怣曽朄
丂
奺榑偲偟偰丄師偺儌僨儖偵娭偡傞婰弎偑偁傞丅
乮1乯崅夝憸搙戝婥儌僨儖
NCAR奐敪偺CCM3.6.6傪梡偄偨崅夝憸搙僔儈儏儗乕僔儑儞寢壥
乮2乯崅夝憸搙奀梞儌僨儖
POP乮Parallel Ocean Program乯傪梡偄偨0.1搙奿巕偺僔儈儏儗乕僔儑儞寢壥丅塹惎偵傛傞娤應寢壥偲斾妑偟偰偄傞丅
乮3乯奀昘堟儌僨儖
婥岓僔儈儏儗乕僔儑儞偵偍偗傞奀昘堟儌僨儖偺廳梫惈傪帵偡婰弎偲儘僗傾儔儌僗崙棫尋媶強偱奐敪偝傟偨CICE乮Sea Ice Model乯偵傛傞僔儈儏儗乕僔儑儞寢壥
乮4乯暲楍婥岓儌僨儖乮PCM丗Parallel Climate Model乯
戝婥奀梞寢崌儌僨儖PCM乮CCM3亄POP亄夵椙儌僨儖乯偺奐敪
乮5乯嬊強儌僨儖
丂
3.4.3.3丂悢抣儌僨儖偺奐敪偵偮偄偰
丂
擔杮偵偍偄偰傕丄抧媴曄摦偺夝柧傪栚昗偲偟偨尋媶慻怐偑敪懌偟偰偄傞乵5乶丅偦偙偱偼丄
乮1乯傾僕傾丒懢暯梞堟偵偍偗傞婥岓曄摦偺梊應
乮2乯傾僕傾抧堟偵偍偗傞悈弞娐偺梊應
乮3乯抧媴壏抔壔偺梊應
乮4乯傾僕傾丒懢暯梞堟偵偍偗傞戝婥慻惉曄摦偺梊應
乮5乯傾僕傾抧堟偵偍偗傞惗懺宯偺曄摦偺梊應
乮6乯抧媴撪晹曄摦儊僇僯僘儉偺夝柧
偑嬶懱揑栚昗偲偟偰愝掕偝傟偰偍傝丄師悽戙偺悢抣儌僨儖奐敪傕娷傑傟偰偄傞丅悢抣儌僨儖偼崱屻偺尋媶偵寚偔偙偲偺弌棃側偄尋媶庤抜偱偁傞偑丄崅惈擻寁嶼傪峴偆忋偱偼暲楍寁嶼婡偺棙梡媄弍丄傕偭偲尵偆側傜偽暲楍寁嶼婡偦偺傕偺偺抦幆偑昁梫偱偁傝丄寁嶼婡壢妛幰偲偺楢実偑廳梫偲側偭偰偄傞丅
偟偐偟側偑傜丄暷崙偲斾妑偟偰擔杮偼僜僼僩僂僃傾奐敪偺廳梫惈偺擣幆丄戝婯柾崅惈擻寁嶼傊偺梫媮偑掅偄傛偆偵姶偠傜傟傞丅偲傝傢偗丄揔愗側墳梡僜僼僩僂僃傾奐敪懱惂傪庢傞偙偲偑偱偒偢丄墳梡暘栰偺尋媶幰偲寁嶼婡壢妛暘栰偺尋媶幰偺嫤椡娭學偑抸偗側偄傛偆偵巚偆丅
暷崙偱偼丄婛偵弎傋偨傛偆偵DOE偩偗偱傕婥徾丄婥岓暘栰偺悢抣僔儈儏儗乕僔儑儞偑慻怐娫偺楢実偺壓丄傑偨偼DOE埲奜偺慻怐偲偺楢実傪庢傝側偑傜丄惛椡揑偵尋媶奐敪偑幚巤偝傟偰偄傞丅偦傟傜偺奐敪偺懡偔偼暷崙偺尋媶僐儈儏僯僥傿偵偍偗傞悢抣僔儈儏儗乕僔儑儞偺偨傔偺嫟捠婎斦儌僨儖乮僐儈儏僯僥傿儌僨儖乯偲尵偊傞傕偺偱偁傞丅SC99乮暷崙億乕僩儔儞僪乯偺僷僱儖摙榑偵偍偄偰丄俀偮偺僐儈儏僯僥傿儌僨儖峔抸偺徯夘偑偁偭偨偑丄暷崙偱偼僐儈儏僯僥傿儌僨儖傪嫟摨偱奐敪偟丄偦傟傪堢惉偡傞懱惂偑庢傟傞傛偆偱偁傞丅
丂
丂俀偮偺僐儈儏僯僥傿儌僨儖偺撪丄堦偮偼塅拡婥徾妛暘栰偺NSF僾儘僕僃僋僩GEM乮Geospace Environment Modeling乯寁夋偱奐敪偝傟偰偄傞GGCM偱偁傝丄懢梲晽偺抧媴廃曈晹偱偺嫇摦夝柧偲塅拡婥徾梊應傪峴偆偨傔偺僔儈儏儗乕僔儑儞儌僨儖偱偁傞丅傕偆堦偮偼丄抧恔婡峔偺夝柧傪栚揑偵奐敪偝傟偰偄傞抧恔偺戝婯柾悢抣僔儈儏儗乕僔儑儞儌僨儖GEM偱偁傞丅GEM偱偼丄僆僽僕僃僋僩巜岦僾儘僌儔儈儞僌偺峫偊曽傪庢傝擖傟丄寁嶼庤朄偲偟偰Fast multipole method丄俁師尦桳尷梫慺朄丄揔墳揑奿巕惗惉朄傪梡偄偰偄傞丅
丂
懠曽丄擔杮偱偼僐儈儏僯僥傿儌僨儖偺奐敪懱惂偑庢傟側偄丅墳梡暘栰偺尋媶幰偲崅惈擻寁嶼暘栰偺尋媶幰偺楢実偼偦偺廳梫惈偑擣幆偝傟偰偍傜偢丄暲楍寁嶼偺偨傔偺僾儘僌儔儈儞僌偼寁嶼婡儊乕僇偺SE棅傒偵側偭偰偄傞偺偑尰忬偱偁傞丅偙傟偼丄徣挕娫傗尋媶僐儈儏僯僥傿偺暻丄奐敪僜僼僩僂僃傾偺強桳尃婣懏偺栤戣摍丄暋嶨側栤戣偵堦晹埶傞偲偙傠偑戝偒偄丅傑偨丄嫮椡側儕乕僟偑寚擛偟偰偄傞丅傛傝崅惈擻寁嶼傪捛媮偟偰偄偔忋偱偼丄墳梡僜僼僩僂僃傾奐敪懱惂傪惍旛偟偰偄偔偙偲偑朷傑傟傞丅
丂
3.4.3.4丂傑偲傔
丂
崱夞偺曬崘彂傪傑偲傔傞偵偁偨偭偰丄暷崙偺婥岓儌僨儖偵娭偡傞帒椏傪撉傒曉偟偨丅奣偟偰丄僷儞僼儗僢僩摍偼傢偢偐側惉壥傪戝偘偝偵婰弎偡傞偺偑晛捠偱偁傝丄幚嵺偳偺掱搙桳岠側僜僼僩僂僃傾奐敪偑峴傢傟偰偄傞偐偼柧傜偐偱側偄偑丄墳梡僜僼僩僂僃傾奐敪僾儘僕僃僋僩偺婙偺壓丄尋媶幰偑嶲廤偟丄嫤椡偟側偑傜惉壥傪弌偟偰偄偔懱惂傪庢偭偰偄傞偙偲偵偼姶怱偟偰偄傞丅
墳梡僜僼僩僂僃傾奐敪偺廳梫惈傪擣幆偟偮偮丄朷傑偟偄奐敪懱惂丄奐敪傪儕乕僪偱偒傞恖嵽偺堢惉丄奐敪帒嬥偺搳擖曽朄偵偮偄偰尒捈偡昁梫偑偁傞偲巚偆丅
丂
嶲峫暥專
[1] 嶰懞丆抧媴壏抔壔偺塭嬁丆婥徾42.9 (1998)
[2] 恀撶丆抧媴壏抔壔梊應偺尰忬丆婥徾42.8 (1998)
[3] 栘杮丆悽奅奺抧偱敪惗偡傞堎忢婥徾丆婥徾43.9 (1999)
[4] 摗媑丆堎忢婥徾偺幮夛宱嵪傊偺塭嬁丆婥徾43.10 (1999)
[5] 徏栰丆抧媴僼儘儞僥傿傾尋媶僔僗僥儉偺敪懌丆揤婥丆Vol.45, No.4 (1998)
丂
嶰旽揹婡丂揷拞廏弐丂島巘
丂
僱僢僩儚乕僉儞僌偺晛媦偲婰壇憰抲偺掅壙奿壔偐傜丄忣曬棳捠偼偦偺懍搙傕検傕巜悢娭悢揑側憹壛傪尒偣偰偄傞丅椺偊偽僐儞價僯僄儞僗僗僩傾偺拞悤僨乕僞僂僃傾僴僂僗偵偼擔偵壗昐枩傕偺僩儔儞僓僋僔儑儞偑傂偨偡傜懲愊偟丄偦偺夝愅傪偡傞偵偁偨偭偰偝傑偞傑側壽戣偑惗偠偰偄傞丅棟榑揑偵偼丄廬棃偺摑寁庤朄傪巊偊偽丄僨乕僞偑偁傟偽偁傞偩偗嫮椡側悇掕偑偱偒傞偙偲偵側偭偰偄傞丅偟偐偟幚嵺偼偦偆娙扨側榖偱偼側偄傜偟偄丅栤戣偼丄摑寁庤朄偱傕妛廗庤朄偱傕壗傪巊偆偵偟偰傕丄偲偵偐偔梊應傪偡傞丄偡側傢偪惓夝偲夁嫀帠椺偑堦弿偵奿擺偝傟偰偄傞僨乕僞傪尦偵丄僷僞乕儞傪尒偮偗丄怴偨側帠椺偱惓夝傪弌偡丄偦傟偵偼偳偆偡傞偐丄偲偄偆揰偵恠偒傞丅偦傟偵偼壗僥儔僶僀僩傕偺崅懍張棟偲偄偆検偺暻偲丄恀偵桳梡側僷僞乕儞偺拪弌偲偄偆幙偺暻傪忔傝墇偊偰丄巰憼僨乕僞傪嵿嶻偵曄偊傞媄弍偑媮傔傜傟偰偄傞丅慜幰偼傑偝偵崅惈擻僐儞僺儏乕僞偺巇帠偱偁傝丄屻幰偼恖娫偲崅惈擻僐儞僺儏乕僞偺嫤摨嶌嬈偵側傞偩傠偆丅
杮崁偱偼丄僨乕僞儅僀僯儞僌偲屇偽傟偰拲栚傪廤傔偰偄傞丄忋婰偺傛偆側戝検僨乕僞偵婎偯偔梊應栤戣偵偮偄偰丄嵟嬤偺尋媶摦岦傪娙扨偵徯夘偡傞丅偦偟偰昅幰傜偺丄僥儔僶僀僩側偳偲偼偲偰傕尵偊側偄彫婯柾側恖娫偲僷僜僐儞偺嫤摨嶌嬈偺椺偲偟偰丄寬峃恌抐僨乕僞偲婥徾僨乕僞偺夝愅椺傪徯夘偟丄僨乕僞儅僀僯儞僌嵟戝偺栤戣偲傕尵傢傟傞丄廀梫偵偮偄偰怗傟傞丅
丂
3.4.4.1丂僨乕僞儅僀僯儞僌偺尰嫷
丂
僨乕僞儅僀僯儞僌偵偼梊應偲抦幆敪尒偲偑偁傞偲尵傢傟傞[1]丅梊應栤戣偼帠椺偲夝摎偑儁傾偱拁愊偝傟偨僨乕僞儀乕僗傪慜採偲偟偰偄偰丄栚昗偼偦偺僨乕僞儀乕僗偵偍偗傞夝摎偵憡摉偡傞傕偺傪怴帠椺偐傜摉偰傞偙偲偵偁傞丅偦偟偰僨乕僞儀乕僗偁傞偄偼暘栰偺抦幆偑枹惍棟偱梊應偵偼晄廫暘側応崌丄抦幆敪尒栤戣偲屇偽傟傞傛偆偱偁傞丅傾僾儕僆儕朄[2]偼僨乕僞儅僀僯儞僌棳峴偺偒偭偐偗傪嶌傝丄暲楍張棟媄弍傕峀偔尋媶偝傟丄検偺暻傊偺挧愴偑傕偭偲傕恑傫偱偄傞偲峫偊偰傛偄偑丄偙傟偼抦幆敪尒栤戣偺夝朄偱偁偭偰丄梊應偺慜抜奒偱偁傞偵偡偓側偄丅
堦曽丄梊應朄偲偟偰拲栚偝傟偰偄傞偺偼丄暘椶栤戣偱偼僒億乕僩儀僋僞乕儅僔儞[3]丄僶僊儞僌傗僽乕僗僥傿儞僌偵戙昞偝傟傞僐儈僢僥傿乕妛廗[4,5]丄帪宯楍梊應栤戣偵偍偄偰偼GARCH朄[6]偱偼側偄偐偲巚傢傟傞丅昅幰傜偼帪宯楍梊應栤戣偵塀傟儅儖僐僼儌僨儖[7]傪揔梡偡傞曽岦偱尋媶傪峴偭偰偄傞丅
丂
3.4.4.2丂寬峃恌抐僨乕僞儅僀僯儞僌
丂
杮椺偼傑偝偵僨乕僞儀乕僗傕暘栰偺抦幆傕枹惍棟偱梊應偵偼晄廫暘側丄抦幆敪尒栤戣偺椺偱偁傞丅懳徾偵峫偊偨偺偼丄敿擭偵堦搙偺掕婜寬峃恌抐偵偍偗傞奺庬専嵏寢壥偲丄偦偺嵺偵夞廂偝傟傞惗妶廗姷傾儞働乕僩偱偁傞丅杮奿揑偵廂廤偡傟偽悢愮恖偺寢壥傪悢擭暘偲偄偆僆乕僟乕偼壜擻偩偭偨偑丄偲傝偁偊偢5000恖暘偁傑傝傪庁傝偰丄傾僾儕僆儕朄傪庒姳夵椙偟偦偺昡壙傪峴偭偨丅
堦斒偵僨乕僞儅僀僯儞僌偼丄僨乕僞偺妉摼丄嶍尭丄僨乕僞偐傜偺儖乕儖拪弌丄儖乕儖偺嶍尭傗夝庍丄偦偟偰儖乕儖揔梡偺俆抜奒偐傜側傞偲尵傢傟偰偄傞丅杮復偱偼偦偺弴偵娙扨偵庤朄偲寢壥偺徯夘傪峴偆丅
丂
懳徾僨乕僞悢偼5770儗僐乕僪丄懏惈悢561偱丄偦偺戝敿偼傾儞働乕僩崁栚夞摎乮乽偄偮傕乿乽偲偒偳偒乿乽偄偄偊乿偐傜偺嶰幰戰堦乯偱偁傞丅偙偙偐傜丄僨乕僞偺僋儕乕僯儞僌偲偟偰5770儗僐乕僪偡傋偰偵偍偄偰抣偺婰弎偝傟偰偄側偄懏惈丄抣偑1庬椶偺懏惈側偳丄懏惈弌尰昿搙偺娤嶡偵偼晄梫偲巚傢傟傞傕偺傪庢傝彍偄偨丅偙偺偲偒偼丄専嵏丒傾儞働乕僩丒捛壛専恌丒懱椡應掕側偳偺暋悢偺懏惈廤崌偛偲偵梡堄偝傟偨僨乕僞偐傜丄庤娫傪偐偗偰旐尡幰枅偺慡懏惈偵懳墳偡傞挿偄儗僐乕僪傪嶌惉偟偨丅偟偐偟屻偺暿僨乕僞偐傜偺摨條側嶌嬈偲偺嫟捠惈傪専摙偟偨寢壥丄懏惈廤崌幆暿巕丄旐尡幰幆暿巕丄懏惈廤崌偵懳墳偟偨抣廤崌偺嶰幰偐傜側傞儗僐乕僪傪嶌惉偡傞偺偑丄傾僾儕僆儕朄偺傛偆側懏惈抣偺摨帪弌尰昿搙傪娤嶡偡傞傛偆側儖乕儖拪弌偵偼揔偟偰偄傞偲偺寢榑傪摼偰偄傞[8]丅
丂
検偺暻傊偺挧愴帺懱傕廳梫偩偑丄暪偣偰僨乕僞検偺嶍尭偺廳梫惈傕巜揈偝傟傞丅偙傟偼幙偵傕塭嬁偡傞杮幙揑側傕偺偱偁傞丅僨乕僞嶍尭偼僨乕僞悢偺嶍尭丄僨乕僞偺懏惈偺嶍尭丄僨乕僞懏惈偺傕偮抣偺庬椶偺嶍尭偺俁庬椶偐傜側傞丅寬峃恌抐僨乕僞偵偍偄偰偼丄慜弎偺傛偆側嵟掅尷偺懏惈嶍尭傪偟偨忋偱丄楢懕抣偺棧嶶壔傪儐乕僓偲懳榖揑偵幚巤偡傞偙偲傪帋傒偨丅僨乕僞偺暯嬒偲昗弨曃嵎偐傜摼傜傟傞揔摉側僨僼僅儖僩偺棧嶶壔梡鑷抣傪儐乕僓偵採帵偟丄儐乕僓偼偦傟傪忋彂偒偱偒傞丅専嵏寢壥偺拞偱堎忢抣斖埻偑婛抦偺傕偺傪丄偙偺婡擻傪梡偄偰廋惓偟偨丅偝傜偵丄晄寬峃側旐尡幰偵懳徾傪偟傏傞傋偔丄専嵏寢壥偺昿搙傪暘愅偟偰俋埲壓偺傕偺傪偡傋偰嶍彍偟偰幚尡傪峴偭偨丅
丂
儖乕儖拪弌偵偮偄偰偼丄傾僾儕僆儕朄傪夵椙偟偰梡偄偨[9]丅僨乕僞嶍尭傪揙掙揑偵峴偭偨偨傔Pentium Pro 200MHz偐傜PentiumIII 400MHz掱搙偺寁嶼婡傪梡偄偰悢暘偲偄偆掱搙偺栤戣偵側偭偨丅偪側傒偵僨乕僞嶍尭傪峴傢側偄応崌偼丄悢擔乣1廡娫偐偐傞丅
丂
儖乕儖偼丄傾僾儕僆儕朄偺僷儔儊乕僞愝掕偵傕傛傞偑丄悢枩偺僆乕僟乕偱摼傜傟偨丅偙偺拞偐傜桳梡側儖乕儖偩偗傪巆偡曽朄偲偟偰丄儐乕僓偵傛傞儖乕儖嶍尭偲儖乕儖専嶕偺庤抜傪梡堄偟偨丅儐乕僓偑堦搙尒偰晄梫偲敾抐偟偨儖乕儖傪嶍彍偡傞僼傿儖僞乕傗丄儖乕儖偱尵媦偡傞崁栚偑屳偄偵曪娷娭學偵偁傞応崌偵丄婎弨傪愝偗偰堦曽傪嶍彍偡傞曽幃傪帋嶌偟偨丅
丂
摼傜傟偨儖乕儖偼嶻嬈堛偵妋擣傪媮傔丄桳梡偦偆偵尒偊傞儖乕儖偑偄偔偮偐偁傞偲偄偆巜揈傪偟偰傕傜偭偨丅敀寣媴悢偲媔墝廗姷偺娭學側偳丄専嵏偲惗妶廗姷偺娭學傪帵偟偨儖乕儖偵偼桳梡側傕偺偑懡偦偆偩偲偄偆尒捠偟偼摼傜傟偨丅偟偐偟側偑傜丄儖乕儖偺宍幃揑側嶍彍偱偼彍偗側偄戝検偺乽偁偨傝傑偊乿偺儖乕儖偵慾傑傟丄恀偵桳梡側儖乕儖傪巜揈偟偮偔偡偙偲偼偱偒側偐偭偨丅
丂
丂
崅搙20km晅嬤偺斾妑揑晽懍偺庛偄惉憌寳偵旘峴慏傪晜偐傋丄偦偙傪柍恖婎抧偲偟偰嬊強揑側娤應傗忣曬捠怣拞宲偵栶棫偰傛偆偲偄偆寁夋偑偁傞[10]丅偙偺傛偆側旘峴慏偺塣峲丄掆棷丄夞廂偵偼丄晽懍偺梊應偑晄壜寚偱偁傞丅偙偺梊應偵梡偄傞偙偲偺偱偒傞僨乕僞偵偼丄抧昞晅嬤偵娭偟偰偼傾儊僟僗丄婥徾儗乕僟丄GPV[11]側偳偑偁傝丄崅憌偵偮偄偰偼崅憌婥徾娤應僝儞僨[12]偲丄怣妝偵偁傞MU儗乕僟[13]偲偑偁傞丅偙偺拞偐傜擖庤偺梕堈側崅憌婥徾娤應僝儞僨偵婎偯偒丄晽懍梊應栤戣傪愝掕偟偰幚尡傪峴偭偨[14]丅
婥徾挕偑婥徾嬈柋巟墖僙儞僞乕傪捠偠偰岞奐偟偰偄傞娤應帒椏CDROM偵偼丄婥徾儘働僢僩娤應偱摼傜傟偨崅搙20倠倣乣栺60倠倣偵偍偗傞婥壏丒晽岦丒晽懍摍偺帒椏傗丄擔杮崙撪偺崅憌婥徾娤應姱彁偵偍偗傞儗乕僂傿儞僝儞僨娤應偲儗乕僂傿儞娤應偱摼傜傟偨娤應帒椏側偳偑廂榐偝傟偰偄傞丅偙偺拞偐傜儗乕僂傿儞僝儞僨娤應偵傛傞忋嬻栺30倠倣傑偱偺巜掕婥埑柺偵偍偗傞晽懍娤應寢壥傪夝愅偵梡偄偨丅
摑寁庤朄偵偼嬒幙側曣廤抍傪慜採偲偟偨傕偺偑懡偄偑丄曣廤抍偺嬒幙惈偵婎偯偐側偄僨乕僞儌僨儖傪梡偄偨夝愅庤朄傕傛偔梡偄傜傟傞丅椺偊偽暋悢偺惈幙偺僨乕僞偑崿崌偟偨曣廤抍傪憐掕偡傞傕偺偑偁傝丄壒惡擣幆偺暘栰側偳偱傛偔巊傢傟偰偄傞丅偙偺傛偆側崿崌曣廤抍儌僨儖偺拞偱丄嬒幙偲傒側偣傞僨乕僞廤抍傂偲偮傂偲偮傪丄杮峞偱偼梫慺曣廤抍偲屇傇偙偲偵偡傞丅崿崌曣廤抍儌僨儖偵偍偄偰悇掕偡傋偒僷儔儊乕僞偼丄嬒幙偲傒側偣傞奺梫慺曣廤抍偺暯嬒傗昗弨曃嵎偲丄偦傟傜梫慺曣廤抍偺崿崌斾偵側傞丅偙偺傛偆側梫慺曣廤抍偺惈幙偲偙偺崿崌斾偲傪摨帪偵媮傔傞曽朄偲偟偰丄EM朄乮Expectation Maximization Algorithm, 婜懸抣嵟戝壔朄乯偑抦傜傟偰偄傞[15]丅
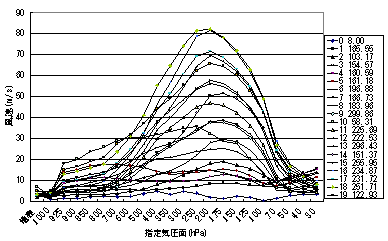
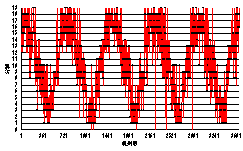
幚尡偱偼崿崌曣廤抍儌僨儖偵懳妏嫟暘嶶崿崌僈僂僔傾儞儌僨儖傪慖戰偟偨丅偙傟偼奺梫慺曣廤抍偑嫟暘嶶惉暘偺側偄懡師尦惓婯暘晍傪偲傞偲偄偆丄崿崌曣廤抍儌僨儖偺拞偱偼旕忢偵扨弮側儌僨儖偱偁傞丅寢壥偺椺偲偟偰丄崅憌婥徾娤應僨乕僞傪崿崌悢20偱暘椶偟偨寢壥傪恾1偵帵偡丅偙傟偼巜掕婥埑柺22儢強偺晽懍丄寁3652夞暘偺僨乕僞傪20庬椶偵暘椶偟偨傕偺偱偁傞丅恾1偵偍偄偰丄墶幉偼巜掕婥埑柺丄廲幉偵偼晽懍傪偲偭偰偄傞丅杴椺偺晹暘偺悢帤偼壗夞暘偑偦偺暘椶偵婣懏偡傞偐傪昞偟偰偄傞丅
傑偨丄奺僨乕僞偑偳偺梫慺曣廤抍偵懏偡傞妋棪偑嵟傕崅偄偐偵傛偭偰暘椶婣懏傪寛傔丄僨乕僞傪暘椶偺曄慗偺宍偵捈偟偰恾2偵帵偡丅恾2偱偼墶幉偵5擭暘偺帪宯楍傪偲傝丄廲幉偵20庬椶偺暘椶傪暯嬒晽懍偺弴偵暲傋偰偄傞丅
丂
 |
||
 |
丂
恾1丂幁帣搰忋嬻1993乣1997擭偺晽懍暘晍偺20暘椶寢壥乮嵍乯
恾2丂幁帣搰忋嬻1993乣1997擭偺晽懍暘晍偺20暘椶偺曄慗乮塃乯
丂
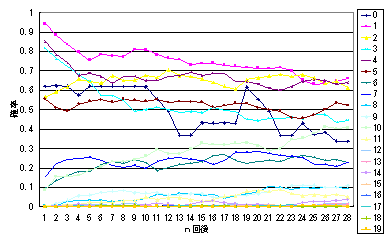
恾2偱帵偟偨暘椶曄慗偼奺暘椶偑妋棪揑側弌椡暘晍傪帩偮偺偱丄偙偺忋偱儅儖僐僼惈傪壖掕偟偨夝愅丄椺偊偽乽偁傞暘椶偺x夞屻偺暘椶乿偺暘晍傪挷傋傞偙偲偼丄塀傟儅儖僐僼儌僨儖[7]傪憐掕偟偰夝愅偟偰偄傞偙偲偵側傞丅偙偺暘晍偐傜丄偁傞暘椶偵懏偡傞僨乕僞偺x夞屻偺僨乕僞偵偮偄偰嬫娫悇掕偑偱偒傞丅恾3偼偦偺椺偲偟偰丄恾1傗恾2偺20暘椶偵婎偯偒丄奺暘椶偐傜侾夞屻乣28夞屻偵偳偺暘椶偵側傞偐傪偧傟偧傟廤寁偟偰丄偦偺斾棪傪梡偄偰1夞屻乣28夞屻偵晽懍偑抧昞偐傜崅搙20km傑偱偵傢偨偭偰20m/s埲壓偱偁傞妋棪傪帵偟偨丅恾3偵傛傟偽丄侾夞屻偵偼暘椶1,3,4偑80乣95%丄堦曽28夞屻偵偼暘椶1,2,4偑60乣65%偺崅偄妋棪傪帵偟偰偄傞丅嵟傕暯嬒晽懍偺掅偄暘椶0偵懏偡傞俉夞偼丄幚嵺偵晽偺庛偄帪偲丄娤應晄擻偱0偑婰榐偝傟偰偄傞帪偑崿嵼偟偰偄傞偙偲偑恾2偐傜塎偊傞丅
 |
丂
恾3丂20偺暘椶偺偦傟偧傟偵偮偄偰n夞屻偺娤應偱慡娤應抣偑20m/s埲壓偱偁傞妋棪
丂
丂
杮愡偱偼僨乕僞儅僀僯儞僌偺堦幚巤椺偲偟偰丄寬峃恌抐僨乕僞偲婥徾僨乕僞偺夝愅椺傪徯夘偟偨丅寬峃恌抐僨乕僞偵傾僾儕僆儕朄傪揔梡偟偨椺偱偼丄僨乕僞嶍尭傪揙掙揑偵峴偭偨偨傔Pentium Pro 200MHz偐傜PentiumIII 400MHz掱搙偺寁嶼婡傪梡偄偰悢暘偲偄偆掱搙偺栤戣偵側偭偨偑丄嶍尭傪偟側偐偭偨応崌偵偼偡偖悢擔傪梫偡傞婯柾偲側偭偨丅偙傟傪椺偊偽婇嬈廬嬈堳慡堳傪懳徾偵偡傞偩偗偱丄寁嶼婡傊偺梫媮惈擻偼悢寘偼偹偁偑傞丅偨偩丄傾僾儕僆儕朄偵戙昞偝傟傞抦幆敪尒抜奒偺庤朄偼丄嬶懱揑墳梡傑偱偵傕偆堦抜奒昁梫側偙偲偑傎偲傫偳偱丄尰抜奒偱偼儐乕僓傪尒偮偗傞偺偑崲擄偲偄偆栤戣偑偁傞丅幚嵺丄僨乕僞儅僀僯儞僌偱惉岟偟偰偄傞婇嬈偼丄暿偺惢昳摍偺晅懏暔偲偟偰埖偭偰惉岟偟偰偄傞偩偗偲傑偱尵傢傟偰偄傞丅暿偺惢昳偲偼椺偊偽丄崅惈擻暲楍寁嶼婡偱偁偭偨傝丄崅惈擻僨乕僞壜帇壔僜僼僩僂僃傾傗僌儔僼傿僋僗儅僔儞偱偁偭偨傝丄摑寁僷僢働乕僕偱偁偭偨傝丄宱塩僐儞僒儖僥乕僔儑儞嬈柋偩偭偨傝偡傞丅偙偺偙偲偐傜丄僨乕僞儅僀僯儞僌偼働乕僉偺僠僃儕乕偵夁偓側偄偲偄偆尵傢傟曽傕偡傞丅堦曽丄婥徾僨乕僞傪椺偵偲偭偨梊應栤戣偼丄偦偺傑傑墳梡偑尒偊傞偨傔丄廀梫偑崅偔儐乕僓偑偮偒傗偡偄偲峫偊傜傟傞丅婥徾僨乕僞偵尷偭偨榖偱傕丄崱屻嬊抧梊曬傗峲嬻梊曬偺暘栰偵廀梫偑崅傑傞偲梊憐偝傟偰偍傝丄偦偺嵺偵偼崱夞偲偼寘堘偄偵戝検偺娤應僨乕僞偵偮偄偰摨條偺夝愅傪峴偆昁梫偑敪惗偡傞偲婜懸偝傟偰偄傞丅
丂
[1] Weiss, S.M. and Indurkhya, N. Predictive Data Mining. Morgan Kaufmann Publishers Inc. (1998).
[2] Agrawal, R. Apirori. (1993).
[3] Schoelkopf,Burges & Smola(Ed.) Advances in Kernel Methods. The MIT Press. (1999).
[4] Breiman, L., Bagging Predictors. Machine Learning. 24 (2)123-140, (1996).
[5] Freund, Y. and Schapire, R.E., Experiments with a New Boosting Algorithm. Proc. of the Thirteenth Intl. Conf. on Machine Learning, Morgan Kaufmann, San Francisco, California. pp.148-156, (1996).
[6] 嶰塝. 僨儕僶僥傿僽偺悢棟. 椪帪暿嶜悢棟壢妛SGC儔僀僽儔儕6. 僒僀僄儞僗幮. (1999).
[7] 拞愳. 妋棪儌僨儖偵傛傞壒惡擣幆. 揹巕忣曬捠怣妛夛. (1988).
[8] 揷拞懠. 僨乕僞儅僀僯儞僌偺偱偒傞僨乕僞宍幃偵偮偄偰. 僨乕僞岺妛尋媶夛(1999).
[8] 嶰愇懠. Knodias偵偍偗傞僨乕僞儅僀僯儞僌曽幃. 戞56夞忣張慡崙戝夛 (1998).
[9] 戞1夞惉憌寳僾儔僢僩僼僅乕儉儚乕僋僔儑僢僾梊峞廤(1999)
[10] http://www.jmbsc.or.jp/乮婥徾嬈柋巟墖僙儞僞乕乯
[11] 崅憌婥徾娤應僨乕僞乮CDROM晅懏儅僯儏傾儖乯
[12] 淎揷. 婥徾夝愅妛. 搶嫗戝妛弌斉夛. (1999).
[13] 揷拞. 崅憌戝婥偺晽懍夝愅偲梊應. 忣張 悢棟儌僨儖壔偲栤戣夝寛尋媶夛 99-MPS-26 (1999).
[14] McLachlan, G.J. and Krishnan, T. The EM Algorithm and Extensions. John Wiley & Sons, Inc. (1997).