--15puzzle問題の探索方法--
-15puzzleの探索-
ここでは、15パズル問題の最短手を求める探索方法
について説明する。
最短手数については
こちら。
8パズルでは、最も難しい状態であっても31回の移動ですむことから、
幅優先探索などを用いて解くことが可能かもしれない。
ただし、15パズルのように盤面がより多くなってくる場合は、
最長手がより長くなり(15パズルの場合は80)探索する状態が
指数関数的に増加する。
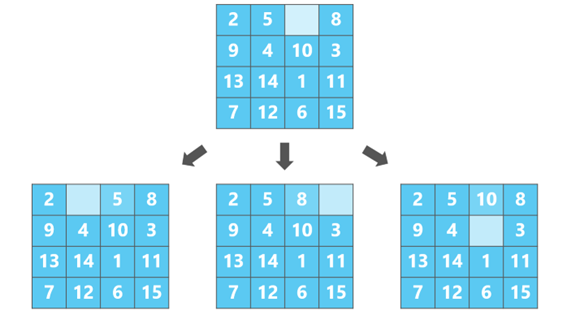
そのため一般的には、15パズル、その他のスライディングパズルを解く
際に用いられる探索方法はA*探索、またはそれを改良したアルゴリズムであることが多い。
以下に、これらのアルゴリズムについて紹介する。
-幅優先探索-
幅優先探索(BFS)は、特定のツリーデータ構造を検索するための
アルゴリズムです。ルートから開始し、現在の深さのすべてのノードを
調べてから、次の深さレベルのノードに移動する。
この探索方法は深さを基準として探索をするため、
15パズル問題など、状態数が多い問題において非常に
大きな時間が掛かってしまう可能性があり、現実的な時間で
解けることはあまり期待できない。よって、以下に示すような探索方法を用いる事が多い。
-A*探索-
A*探索アルゴリズムは最短経路を見つけるアルゴリズムであり、
ヒューリスティック関数を用いて探索を行う。
ヒューリスティック関数とは,最も近いゴールノードまでのコストの推定値
を求める関数であり、このヒューリスティック関数によって探索の効率が大きく変わる。
-ヒューリスティック関数-
ヒューリスティック関数は以下のようなものがある。
・違うタイルの枚数
最も簡単に考えられるヒューリスティックとして、違うタイルの枚数が挙げられる。
しかし、これは違うタイルの枚数の情報のみであることから
効果はあまりでないことが考えられる。
・マンハッタン距離
マンハッタン距離は、現在位置と目標位置の差をそれぞれのタイルで計算し、
それを合計した値を用いる。これは、各タイルが目的の状態までに動かなければ
ならない動きの最小の値であることが分かる。
・パターンデータベース
PDBテーブルを作成し、それを元に探索を行う方法。データベースには、それぞれの状態について
ヒューリスティックコストが登録されていて、それを用いることで高速に探索することが可能。
80手の対極への最適解はそれぞれ数秒で可能だが、メモリを大量に消費するといった点もある。
