--15puzzle問題の手数について--
-15puzzle問題の最短手数とは-
ここでは15puzzleの最短手数とは、ある15パズルの盤面が存在したときに、
目的の盤面に到達するためにかかる最短の動作の回数のことを指す。
例えば、以下の左の盤面から、右の盤面を目指した際の
最短手数は38手である。
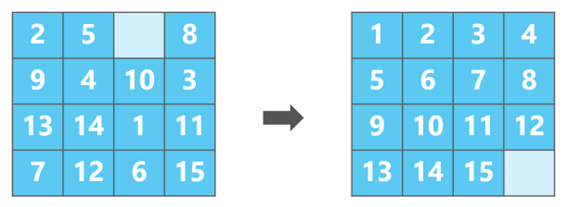
空白のタイルを以下の番号のタイルと入れ替えていくことで到達する
10→1→6→12→7→13→9→2→5→10→1→4→10→1→4→6→12→7→14→10
→2→5→1→2→6→3→11→12→7→15
→12→11→8→4→3→7→11→12
-15puzzleの最短手数について-
15puzzleの最短手数については、どのような状態であっても
最大80手以内に目的の状態に到達できることが分かっている。
また、目的の状態が、上の図の右側の盤面であった場合に、
最短手数が80手である状態は17状態存在する。
最短手数とその最短手数である盤面の状態がいくつあるかの表を以下に示す。
| 手数 | 状態数 |
手数 | 状態数 |
手数 | 状態数 |
手数 | 状態数 |
| 0 | 1 |
21 | 3,098,270 |
42 | 115,516,106,664 |
63 | 105,730,020,222 |
| 1 | 2 |
22 | 5,802,411 |
43 | 156,935,291,234 |
64 | 65,450,375,310 |
| 2 | 4 |
23 | 10,783,780 |
44 | 208,207,973,510 |
65 | 37,942,606,582 |
| 3 | 10 |
24 | 19,826,318 |
45 | 269,527,755,972 |
66 | 20,696,691,144 |
| 4 | 24 |
25 | 36,142,146 |
46 | 340,163,141,928 |
67 | 10,460,286,822 |
| 5 | 54 |
26 | 65,135,623 |
47 | 418,170,132,006 |
68 | 4,961,671,731 |
| 6 | 107 |
27 | 116,238,056 |
48 | 500,252,508,256 |
69 | 2,144,789,574 |
| 7 | 212 |
28 | 204,900,019 |
49 | 581,813,416,256 |
70 | 868,923,831 |
| 8 | 446 |
29 | 357,071,928 |
50 | 657,076,739,307 |
71 | 311,901,840 |
| 9 | 946 |
30 | 613,926,161 |
51 | 719,872,287,190 |
72 | 104,859,366 |
| 10 | 1,948 |
31 | 1,042,022,040 |
52 | 763,865,196,269 |
73 | 29,592,634 |
| 11 | 3,938 |
32 | 1,742,855,397 |
53 | 784,195,801,886 |
74 | 7,766,947 |
| 12 | 7,808 |
33 | 2,873,077,198 |
54 | 777,302,007,562 |
75 | 1,508,596 |
| 13 | 15,544 |
34 | 4,660,800,459 |
55 | 742,946,121,222 |
76 | 272,198 |
| 14 | 30,821 |
35 | 7,439,530,828 |
56 | 683,025,093,505 |
77 | 26,638 |
| 15 | 60,842 |
36 | 11,668,443,776 |
57 | 603,043,436,904 |
78 | 3,406 |
| 16 | 119,000 |
37 | 17,976,412,262 |
58 | 509,897,148,964 |
79 | 70 |
| 17 | 231,844 |
38 | 27,171,347,953 |
59 | 412,039,723,036 |
80 | 17 |
| 18 | 447,342 |
39 | 40,271,406,380 |
60 | 317,373,604,363 |
| 19 | 859,744 |
40 | 58,469,060,820 |
61 | 232,306,415,924 |
| 20 | 1637,383 |
41 | 83,099,401,368 |
62 | 161,303,043,901 |
Korf, R., and Schultze, P. 2005.
Large-scale parallel breadth-first search.
In Proceedings of the 20th National Conference on Artificial Intelligence (AAAI-05),
1380-1385.
