A Brief Introduction to DJ

DJ is an extension of Java that supports constraint programming. It retains the object-oriented feature of Java. A DJ program consists of several classes and optionally several constraint definitions. In addition to field and method declarations, a class can also include dj-field declarations, constraints, and actions.

		  ClassMemberDeclaration::-

		 		  FieldDeclaration

		 		  MethodDeclaration

		 		  DJFieldDeclaration

		 		  Constraint

		 		  Action

The extension to Java's syntax is kept as small as possible. A constraint has similar syntax to that of a conditional expression in Java, and a constraint definition is like a method declaration except that the body is a sequence of constraints. Because of this similarity, people who know Java and constraint programming can master the new language in a very short time. The users can never get confused about constraints and statements because they appear in different contexts.

The DJ system is an interpreter that takes a DJ program and the name of the main class in the program. No class in the program needs to be declared as the main class when the program is written. The interpreter creates an instance of the main class and determines the attribute values of the components that satisfy the constraints. It finally generates a Java applet that displays the components.

DJ can be used not only to draw graphics and build graphical user interfaces but also to solve constraint satisfaction problems in general. For example, the following shows the code for solving the N-queen problem. Figure shows a solution to the 8-queen problem.

 
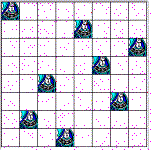
Figure:  A solution to the 8-queen problem.

 class Queens {
     static public final int N = 8;
 
     dj Square board[N][N]{fill==false};
     dj Image queens[N]{name=="queen.gif";
                        size==board[0][0].size};
     dj int pos[N] in 0..N-1;
 	   
     for (i in 0..N-1) samePosition(queens[i],board[i][pos[i]]);
     notattack(pos,N);
     grid(board);
 }
 
 constraint notattack(int[] pos,int N){
     for (i in 0..N-2,j in i+1..N-1){
         pos[i] != pos[j];
         pos[i] != pos[j]+j-i;
         pos[i] != pos[j]+i-j;
     }
 }

N is defined as a constant. The chessboard is represented as a two-dimensional array of unfilled squares and the N queens are represented as an array of images. Every image has the same size as a grid square. We also use an attribute array, called pos, to indicate the positions of the queens. For each queen i, the element pos[i] indicates the number of the row on which the queen is placed.

The for constraint constrains the positions of the images. For each queen i, the image queen[i] and the square board[i][pos[i]] must have the same position. Notice that the index pos[i] is a domain variable. This feature is very powerful. Without this feature, we would have to write the constraint as:

 for (i in 0..N-1, j in 0..N-1)
       pos[i]==j -> samePosition(queens[i],board[i][j]);

The notattack constraint, which is a user-defined one, ensures that no two queens attack each other. The grid constraint constrains the layout for the board. The signature for grid is as follows:

 grid(DJComponent[][] comps)