


Next: Final remarks
Up: COPLAS:
a COnditional PLAnner
Previous: Plans and plan
A goal will consists of a set of properties that we would like to hold
in any situation we reach after the execution of our selected plan.
The plan will be executed starting from an initial situation derived
from the domain description. This situation is unique and is defined
as follows. The initial situation 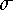 0 for a domain description
D is the situation where every fluent f of a term intially(f) in
D is true in
0 for a domain description
D is the situation where every fluent f of a term intially(f) in
D is true in 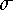 0, every fluent f of a term
intially_unknown(f) in D is unknown in
0, every fluent f of a term
intially_unknown(f) in D is unknown in 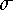 0 and any other
fluent is false in
0 and any other
fluent is false in 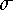 0. It is also assumed that every axiom
holds in
0. It is also assumed that every axiom
holds in 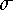 0. If there is no consistent situation with such a
structure or the domain has no models we will say that the domain D
is inconsistent.
0. If there is no consistent situation with such a
structure or the domain has no models we will say that the domain D
is inconsistent.
We will restrict our goals to be a conjunction of fluent literals
denoted by p1 ,..., pn . We say that a plan 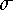 achieves a
goal p1 ,..., pn in a domain D if for every model
achieves a
goal p1 ,..., pn in a domain D if for every model 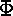 of D, if
each fluent literal in the goal is true in
of D, if
each fluent literal in the goal is true in
 (
(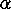 ,
,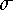 0). That is, for any possible
interpretation that models the domain, the evaluation of the plan
produces a situation where the goal is true.
0). That is, for any possible
interpretation that models the domain, the evaluation of the plan
produces a situation where the goal is true.
We will write
D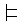 p1 ,..., pn after
p1 ,..., pn after 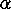
when the plan
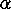 achieves p1 ,..., pn in D. COPLAS takes a consistent domain
description D and a goal, and returns a plan
achieves p1 ,..., pn in D. COPLAS takes a consistent domain
description D and a goal, and returns a plan 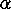 that achieves
the goal, if that plan exists. A formal definition of achievement can
be found in the full report.
that achieves
the goal, if that plan exists. A formal definition of achievement can
be found in the full report.



Next: Final remarks
Up: COPLAS:
a COnditional PLAnner
Previous: Plans and plan
www-admin@icot.or.jp
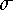 0 for a domain description
D is the situation where every fluent f of a term intially(f) in
D is true in
0 for a domain description
D is the situation where every fluent f of a term intially(f) in
D is true in 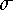 0, every fluent f of a term
intially_unknown(f) in D is unknown in
0, every fluent f of a term
intially_unknown(f) in D is unknown in 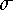 0 and any other
fluent is false in
0 and any other
fluent is false in 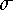 0. It is also assumed that every axiom
holds in
0. It is also assumed that every axiom
holds in 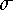 0. If there is no consistent situation with such a
structure or the domain has no models we will say that the domain D
is inconsistent.
0. If there is no consistent situation with such a
structure or the domain has no models we will say that the domain D
is inconsistent.



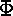 of D, if
each fluent literal in the goal is true in
of D, if
each fluent literal in the goal is true in
 (
(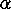 ,
,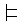 p1 ,..., pn after
p1 ,..., pn after