第3章 ハイエンドコンピューティング研究開発の動向
佐藤 裕幸 委員
1. はじめに
レーダなどのセンサからのデータ処理と言えば、従来は、DSP(Digital Signal Processor)を用いた処理やFFT(Fast Fourier Transform)などの信号処理が中心であった。すなわち、信号レベルでのデータをいかに高速に処理するかが課題であった。一方近年では、信号レベルではなく、より抽象度の高いデータを処理することが多くなってきている。例えば、観測された信号データを位置情報として扱い、目標追尾を行うことが挙げられる。目標追尾とは、レーダ等のセンサの観測結果から目標の航跡を抽出し、位置や速度等の運動諸元を推定する問題である。目標追尾の抱える課題の1つに、追尾目標の近傍に他の目標やクラッタ等の不要信号が存在する高密度環境下での追尾性能の確保が挙げられる。高密度環境下では、センサから得られた観測値のいずれが各追尾目標のものであるかを判定する相関処理が重要となる。この相関処理は、いわゆる組み合わせ問題であり、従来の情報処理の分野で用いられてきた手法が適用でき、それらを用いて高速化・並列化が試みられている。
ここでは、この追尾処理の並列処理を用いた高速化について紹介する。
2. 目標追尾とは
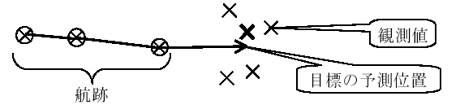
目標追尾とは、レーダ等のセンサの観測結果から目標の航跡を抽出し、位置,速度等の運動諸元を推定する問題である。目標追尾の抱える課題の1つに、追尾目標の近傍に他の目標やクラッタ等の不要信号が存在する高密度環境下での追尾性能の確保が挙げられる。高密度環境下では、センサから得られた観測値のいずれが各追尾目標のものであるかを判定する相関処理が重要となる。従来は、各追尾目標に対して、予測位置に最も近い観測値を選択し、追尾計算に使用する方式が採られていた(図1参照)が、この方式では高密度環境下では追尾性能が不十分であった。そこで、より高度な相関方式を採用した航跡型MHT(Multiple Hypothesis Tracking)[1] が提案された。

図1 NN(Nearest Neighbor)方式による目標追尾
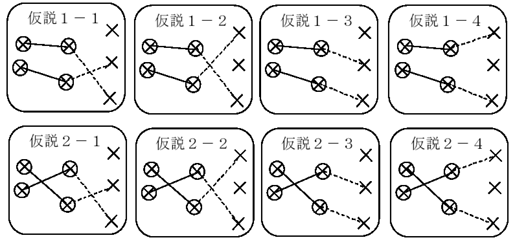
図2 航跡と観測値の組み合わせ
この航跡型MHTでは、観測値の時系列データから成る航跡のいずれが追尾目標であるかについて、他の目標やクラッタが存在する可能性及び追尾目標が探知されなかった可能性も考慮して、複数の仮説を構成しながら追尾処理を行う(図2を参照)。このように複数の仮説を保持しながら処理を進めていくため、追尾精度は優れるが、処理負荷が高く、また仮説の数が組合せ爆発を起こし膨大になる危険性があるという問題点があった。そこで、仮説数を抑制するために、信頼度の高いものから順に固定数の仮説しか生成しないNベスト探索アルゴリズムを用いることで、航跡型MHTが高速化されている[2] [3]。
このNベスト版航跡型MHTにおいて、追尾精度を向上させるには、Nの値、すなわち仮説生成上限数をできるだけ大きくしなければならない。そのためには、生成仮説数を抑えたNベスト版航跡型MHTにおいても、処理の高速化は重要な課題である。そこで、並列処理により、Nベスト版航跡型MHTの高速化を行っている。
3. 航跡型MHTの概要
図3の処理フローに基づいて、航跡型MHTの概要を述べる。
3.1 観測ベクトルの入力
1サンプリング時刻の観測ベクトル(センサによる目標のX,Y,Z座標など)を入力する。
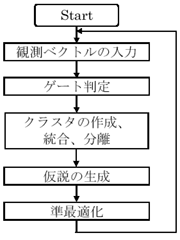
図3 航跡型MHTの処理フロー
3.2 ゲート判定
各サンプリング時刻から高々一つの観測ベクトルを選んだ時系列データ(0観測ベクトルは、目標が探知できない場合を想定)を航跡と呼ぶ。1サンプリング前のどの航跡とどの観測ベクトルが対応しているのかの相関処理を行う範囲をゲートと呼ぶ。すなわち、各1サンプリング前の航跡に対して、現サンプリング時刻の観測ベクトルが存在すると予測される空間の領域をゲートと定め、この領域の観測ベクトルのみ相関処理の対象とする。
3.3 クラスタの作成、統合、分離
互いに観測ベクトルを共有しない航跡の集合をクラスタと呼ぶ。すなわち、航跡TiとTjが少なくとも一つの観測ベクトルを共有する場合に限り、航跡TiとTjを類似航跡と呼び、Ti〜Tjと書く。航跡Ti, Tjにおいて
Ti=Ti1〜Ti2〜…〜Tin-1, Tin=Tj (1)
となるTi1, Ti2, …, Tinが存在する場合に限り
Ti≡Tj (2)
と定義する。各サンプリング時刻の全航跡は、式(2)の関係により、互いに素な複数の部分集合に分けられ、この部分集合をクラスタと呼ぶ。以下の3.4、3.5の処理は、各クラスタ毎に独立して処理することが可能である。
どのクラスタにも属さない観測ベクトル(どの航跡のゲート内にも入らない観測ベクトル)がある場合は、新たにクラスタを生成する。また、異なるクラスタに属する複数の航跡のゲート内に同じ観測ベクトルが入っている場合、それらのクラスタの統合を行う。更に、後述の準最適化処理により過去のデータを捨てた結果、互いの航跡が共有する観測ベクトルを持たなくなった場合は、クラスタを分離する。
3.4 仮説の生成
各クラスタにおいて、0個以上の航跡を選択して構成した航跡の集合を仮説と呼ぶ。各仮説は、クラスタ内のどの航跡の組合せを選ぶのが正しいのかを表わすものであり、最終的に求めたい目標の位置、速度等の運動諸元の基となる解候補である。各仮説を構成する際の基準は、同一仮説内に属する複数の航跡間で観測ベクトルを共有しないように航跡を選択することである。なお、仮説に含まれるどの航跡にも属さないクラスタ内の観測ベクトルは、この仮説において誤信号と扱ったことに相当する。
仮説を生成するには、まず現サンプリング時刻における観測ベクトルの入力を反映した航跡を生成して、それらを選択する。これは、各観測ベクトルが、どの既存の航跡と対応するのか、新たな航跡なのか、誤信号なのかを表わす選択木として考えることができる。
以下に、例を用いて説明する。1サンプリング前のある仮説の航跡がT1及びT2であり、現サンプリング時刻では、航跡T1がゲート内に2つの観測ベクトルZ1及びZ2を捕らえ、航跡T2が1つの観測ベクトルZ2を捕らえている(図4)。この状況下での航跡と観測ベクトルの可能な組合せは、図5に示すような選択木で表わすことができる。この木の根から各葉までを辿る枝がそれぞれの仮説であり、この例では11個の仮説が生成されることになる。
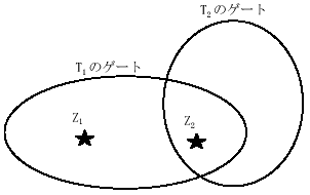
図4 ゲートと観測ベクトル
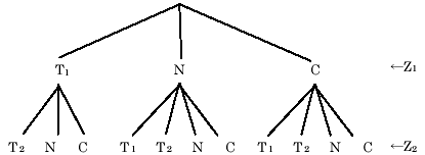
N:新航跡、C:誤信号
図5 航跡と観測ベクトルの組合せ
1つの親仮説から生成される子仮説の数は、その仮説内の航跡と観測ベクトルとの可能な組合せ数になるので、航跡数や観測ベクトル数が少しでも多くなると、直ぐに組合せ爆発を起こしてしまう可能性がある。そこで、仮説の生成段階で信頼度の高いものから所定数しか生成しないようにしている。
前述のように、考えられる仮説は図5のように選択木で表わすこともできるが、各列を誤信号、既存航跡、新航跡、各行を観測ベクトルとし、各要素を信頼度(相関度)とする行列とし、互いに同一の列からの要素を選択しないように各行について1要素ずつ選択することでも、仮説を表わすことができる。そして、選択した各要素の値の総和が最も大きくなるように選択する方法を見つけることが、最も信頼度の高い仮説を生成することになる。このような選択問題を効率的に行うアルゴリズムとしてMunkresのアルゴリズム[5] がある。更に、最高信頼度仮説を生成した後は、選択した枝を境界とする部分木に分割する。例えば図6において、太い枝が選択された仮説であるとすると、その枝を境界とする部分木は、四角で囲った2個所となる。そして、それぞれの部分木で最高信頼度仮説を生成した後、それらの中で最も信頼度が高い仮説を選択する。これを仮説数が規定数Nになるまで繰り返す。この方法をMurtyアルゴリズム[6] と呼び、これにより効率的に高信頼度の仮説から生成することができる。
なお、仮説の信頼度、すなわちその仮説が真である確率は、文献[4] に詳しいが、目標の探知確率、ゲート内捕捉確率、誤信号発生率、新目標発生率、仮説を構成する航跡と対応する観測ベクトルとの相関度及び基となる親仮説の信頼度の項から構成されている。
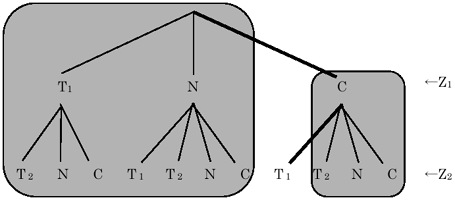
図6 選択木の分割
3.5 準最適化
古いデータを捨てることにより、最新Nサンプリングの観測ベクトル構成が同一である航跡を同一視した結果、内容(構成する航跡)が同一となった仮説同士を統合する。これをNスキャンリミットと呼び、仮説数の抑制を信頼度ではない別の観点で行っていることに相当する。