これまでのアプリケーションの大きな流れから未来の方向を予測する。各アプリケーションで詳細は異なるであろうが、大枠は次のようになっている。
| ・1次元 | −−> | 2次元 −−> 3次元 |
| ・線形 | −−> | 非線型 |
| ・定常解 | −−> | 非定常解(時間的変化) |
| ・1ケースの計算 | −−> | 多くのケースの計算(パラメトリックスタディ、最適化) |
| ・粗いモデル | −−> | 詳細なモデル |
| ・計算能力の向上により、それまでは不可能であった計算方法・新分野が出現する | ||
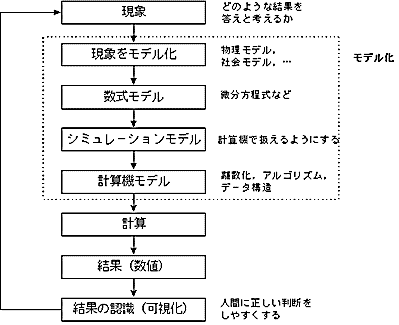
また、計算機を使って問題を解くという原点に戻ると、計算そのものだけではなく、モデル化の問題、アルゴリズム、計算結果を正しく認識させる技術も重要である。基本的なモデリングについては、企業では難しいため、大学や政府の研究所での研究が必要である(図1 計算機で問題を解く手順)。
日米比較では多く(ほとんど)のアプリケーションが欧米製であり、日本はお寒い状況である。上記のモデリングについても、米国、欧州での研究に遅れをとっている。米国の大学の場合、モデルを開発し、それをアプリケーションにのせるまでの仕事を行っている。日本でもそこまでやれるような体制(仕事の評価まで含めて)が必要である。また、すべての分野で欧米と対抗することは不可能であり、日本が得意とする分野で自主性を発揮すべきである。

電子計算機(コンピュ−タ)のアプリケーションは、新たな有用な道具が提供されたことにより、その当時の先進的な科学者、技術者により、ただちに色々な分野への適用の努力が始まった。今のプログラム電卓よりも劣る計算機ではあったが、その当時としては画期的なことであった。いま、科学技術分野に限ってみても、流体、構造、回路、デバイス、材料、化学、天文、気象、地震、プラズマ物理、・・・と計算機が利用されている分野は非常に多く、計算機のアプリケーションの全分野に渡って述べることは不可能なことである。ここでは、あえて独断と偏見に陥ることを恐れず、筆者の関係してきた分野での限られた範囲でアプリケーションの方向と問題点について述べることにする。以下でいくつかの例について述べる。
(1) 共役傾斜法(CG法) の変遷
例えば、科学技術計算で重要な位置を占めている連立一次方程式の解法の1つである共役傾斜法の変遷をたどってみる。連立一次方程式の解法の場合、ガウスの消去法のような直接法は有限回の演算で計算が終了する。しかし、反復法の場合、条件の良い場合は少ない反復回数で収束するが、条件が悪い場合は反復回数が非常に多くなってしまう。普通、反復法の場合、有限回の演算で計算が終了する保証がない。共役傾斜法が出現したころ、反復法で有限回で収束と評判になった。しかし、色々な問題に適用してみたところ、有限回の演算で収束しないケースがあることが判明した。共役傾斜法が有限回の演算で終了するためには、無限桁の計算が必要である。そのため、一時、下火になった。その後、解くべき行列に前処理を施すことにより、収束性が大幅に改善された場合があることが分かり、前処理+共役傾斜法で復活した。偏微分方程式を離散化して得られる行列に前処理を施すことは、もとの問題の性質を利用して、大幅な収束性の改善を得ていることになっている。その結果、計算速度も速くなった。
これは、問題の範囲を限定し、問題の性質を利用することにより、解法の能率を向上させている。いわば、解法(アルゴリズム)の専用化の方向である。
(2) 制御系のシミュレ−ション(連続系シミュレ−ション言語)
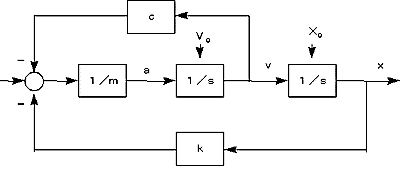
制御系ではモデルをブロックダイアグラムで表現することが多い。ブロックダイアグラムでは機能ボックスを接続するだけで制御モデルを構築することができる(図2 ブロックダイアグラムの例)。いわばオブジェクト指向あるいは関数型的にモデルを構築することができる(非手続き的な表現になっている)。ブロックダイアグラムの結線はアナログ計算機の配線(デジタル計算機のプログラミング)に対応している。計算機が出現したころは、ブロックダイアグラムで表現されたモデルも離散化し、アセンブラ、FORTRANなどで手続き的に計算されていた。その後、IBM 7040/7090の上で問題向き言語(連続系シミュレ−ション言語と呼ばれる)DSL-40/90が開発され、非手続き的に計算をすることが可能となった。連続系シミュレ−ション言語はその後、CSMP-III(IBM 360/370シリ−ズ)、CSPL-6(ACOS-6)、ACSL(多くの機種で稼動)等に発展している。モデルの変更が多い分野では、手続き的表現に比較して、大幅(2〜3桁)な時間節約になる。さらに、最近では機能ブロックのアイコンを選択して、機能ブロック同志を結線することにより、モデルを構成できるアプリケーションが出現している。これは、図形的入力(ブロックダイアグラム)への回帰ということができる。
この例は、間違いにくい記述方法、高いレベルでのモデル記述の重要性を意味している。
(3) モデルの詳細化
モデルの詳細化という面から考える。計算機の性能が低かった時代には、もとの問題をそのまま解くのではなく、何等かの形でパラメタライズされた方法で問題を扱っていた。例えば、半導体の中で、電子の移動度を導入することにより、電子の平均的な動作は扱うことができるが、電子と原子核の相互作用のような効果は扱うことができない。しかし、移動度という概念を導入することにより、計算量を大幅に削減でき、外からの電圧・電流関係が必要な場合は十分な近似になっている。
また、半導体のデバイスシミュレ−ションは、内部動作に関係する電子の数がまだ非常に多いので、主流のソフトでは電子などを流体モデルで近似して、計算を行っている。しかし、構造が微細化してくると、内部動作に関係する電子の数が少なくなり、流体モデルでは実際の現象を十分に近似できなくなる。実際の現象を表現するためには、個々の電子レベルでのモデルを構築する必要がある(粒子モデル)。
最近の材料の設計などでは、第一原理からの分子・原子相互の関係から結果を求めることが行われている。このような計算は、非常に大きな計算能力を必要とするが、ある仮定を入れた計算では現れることにない効果を予測することも可能となる。
今後は、研究の高度化や設計の最適化を行うためには、より詳細なモデルを必要とする場面が多くなる。
(4) 次元の変遷
電子計算機(コンピュ−タ)の多くのアプリケーションは偏微分方程式を数値的に解くという観点から始まっている。偏微分方程式を離散化して解く場合、1次元から始まり、2次元、3次元と進んでいる。今後も、詳細な結果が必要な分野では3次元の取り扱いが不可欠となる。3次元の場合、各次元の分割数を増やすと必要となるメモリ−が急激に多くなる(3乗に比例)。多くのメモリ−を実装した計算機システムを如何に効率的に開発するかが問題となる。
(5) 線形モデルから非線型モデルへ
近似モデルも線形で済んでいた(我慢していた)時代から、非線型が必要な(扱える)時代へと変化している。線形モデルの場合、ある1ケースの結果が分かれば、入力が異なる計算結果も全て予測可能となる。しかし、非線形モデルの場合は、入力と出力が比例関係にはないので、入力が異なると、その入力に対しての計算を再度行わなければならない。非線形計算は1回だけでも線形計算よりも計算量が多いが、その上に、入力と出力の比例関係がないので、より多くの計算が必要になる。
(6) 時間の扱い
時間的な面も定常解ですんでいた(我慢していた)時代から、非定常解が必要な(扱える)時代へと変化している。
(7) パラメトリックスタディ、最適化
計算機の能力が低かった時代には、1ケースだけでも結果が得られることが大切であったが、計算機の能力が大きくなるにしたがって、多くのケースの計算が可能になり、研究・開発の最適化が可能になる。パラメトリックスタディ、最適化、統計的な解析が可能となり、1ケースの計算に比べて多くの知見を与えてくれる。
これからは、人口の減少の時代を迎えると、研究者・技術者の不足といる時代となり、多少無駄な計算をしても、人間の時間を減らす方向に進むであろう(計算機に金を投資し、時間をお金で買う時代となろう)。
(8) 問題解決の重要度の変化
計算の重要部分も変化している。計算機を使って問題を解くということを考えると図1(計算機で問題を解く手順)のようになる。計算機が出現された当初は計算すること自身が時間がかかり、最大の問題点であった。計算機が高速化し、計算手法も高度化することにより、問題解決のフローの中で計算の占める比重が段々低下している。自動車工業での車体の強度解析(衝突解析)では、計算よりもメッシュ作成の比重のほうが大きくなっている。計算は数日あれば終了するが、メッシュ作成には数ヶ月が必要になっている。このような部分にも計算機パワーを利用して短縮することも重要になっている。計算の高速化により、モデル作成(メッシュ)に比重が移る。今後は、ますます、問題解決の全体の時間が重要になり、問題解決の手順の中で最も時間の掛かる部分を速くすることが重要となる(モグラたたき)。そのためには、数値的計算だけではなく、数式処理、人工知能等の非数値的処理も組み合わせて、お互いの良いところを利用し、問題解決の全体の時間を短縮することが重要となる。いわば、問題解決のシームレス化であろう。
今後は、前節のように、多くのポイントでシミュレ−ションの高度化が進展し、それに応じてより大きな計算能力が必要とされる時代になろう。
計算機の能力が大きくなるにしたがい、より良い結果が得られるようになるであろうが、その結果が現実の研究・開発・設計に与える影響は見かけ上、計算機の能力向上と比例しないと予測できる。これまで、計算機の能力・計算手法の進歩により、段々と詳細で精度の良い結果が得られてきているが、その効果はある閾値を越えたところで変革を起こしているようである。計算機の能力が段々大きくなるに従い、定性的結果だけであったものが、定量的結果が得られるようになってきた。定性的結果でも研究・開発・設計の方向を決める知見となり、定量的結果が得られるようになるとシミュレ−ション段階での最適化が可能となる。まず、定性的には正しい結果が得られるようになった時点で第1の変革が起り、その後、定量的に正しい結果が得られるようになった時点で第2の変革が起きるであろう。現在は、定性的に正しい結果は多くの分野で得られるようになり、定量的に正しい結果が得られる分野が出現してきたところであろう。これからの課題は、まだ、定性的結果も得られていない非常に難しい分野でのモデル化やアルゴリズムの確立と、定性的結果が得られている分野でも定量的結果を得られるような努力であろう。定性的結果も得られていない分野はまだ多く存在し、五感に依存している分野の技術化であろう。更に、第六感が必要といわれている分野も解明したいものである。
また、計算機の能力が飛躍的に向上すれば、これまで不可能と思われていた分野、手法も実現可能となり、新たな応用分野が必ず出現するはずである。一方で、使い易さの点も重要であり、飛躍的に向上した計算機の能力を計算以外の部分に振り分けることも重要である。
今後の高性能の計算機を構成するには並列化は不可欠である。そのため、並列化を推進するには、現在、高価な並列計算機の価格を安くする必要がある。 並列計算機を普及させて、価格を低減させることが重要である。そのためには並列化が行い易い分野から、並列化を行うべきである。パラメトリックスタディなどは並列化しやすい分野である。現実的には、疎粒度の問題から手をつけることも必要である。(これは細粒度の並列化を否定しているのではない。並列処理を普及させると細粒度の並列化がより重要になる。まずは並列処理の普及という意見である。)
政府の支援は下記のような基礎的な分野での研究投資が重要である。
また、シミュレ−ション分野ではソフトの重要性が大きく、それも理論的なものだけではだめで、実際に利用可能なレベルまでのソフトの開発が重要である。しかし、日本では大学等でのソフトに対する評価がされていないのが問題である。米国との比較においても最大の問題である。
技術開発にあたり、米国優位となる日米の差はソフト開発に対する評価と新しいソフトに対する先取性の有無であろう。これは、これまで日本が欧米に追いつくことだけに重点をおいてきたことの弊害であろう。
日本が米国に対等もしくは優位の部分の1つは回路シミュレ−ションのエンジン部分である。ベクトル計算機でのベクトル化は日本では約10年前に3社で成功したが、米国ではやっと1〜2年前に成功した状況である。
これまで米国に任せて、日本が手をつけていない分野はほとんどの分野であるとも言える。これまで、日本では手をつけたといっても、欧米の後追いが多く、自主的に手がけた分野は残念ながら少ない。
科学技術分野の「数値シミュレーション」という言葉には、「誰もが扱うことのできる計算機は、 理論解析を補強する道具または実験解析を行う道具であり、道具以上のものではない」という計算機を利用した研究に対する負のイメージが含まれていたように感じられる。
しかし、ここ数年のスーパーコンピュータの飛躍的発展、及び超並列計算機の出現等によって、数値シミュレーション技術を駆使すれば未知現象の解明や実験不可能な現象の解明さえも可能になると考えられており、数値シミュレーションに基づく研究手段が「計算科学」という一つの研究分野を形成しつつある。理論、実験につぐ「第3の科学」と称する計算科学は、さまざまな研究対象について、横断的かつ普遍的な研究手段が提供できるように考えられている。
この過程において、数値シミュレーションに対する負のイメージは払拭された。しかし、計算科学の現状を考えると、理論、実験科学に対抗する手段に到っていない。計算科学がさらに発展するためには、現状よりもさらに高い計算能力を有する超高速計算機が必要なことは明らかである。本稿では、計算科学をより発展させるための超高速計算機開発について考えてみたい。
本ペタフロップスマシン技術調査ワーキンググループの平成8年度の報告書「ペタフロップスマシン技術に関する調査報告」においては、「将来のペタフロップス級のコンピュータは超並列計算機にならざるを得ない」という共通の認識がまとめられている。計算科学に用いられる超高速計算機は、当然分散メモリ型並列計算機であろう。しかしながら、ここ1年間を見ても、分散メモリ型並列計算機の利用技術はさほど進展しておらず、依然として利用技術の研究に留まっており、応用分野の研究者自身が一人で使いこなせる状況にない。これは、単一プロセッサや共有メモリ型計算機などの従来の計算機と同様に、分散メモリ型並列計算機についても広範囲のユーザに提供することを目標にしているからではないだろうか?
並列計算というプログラミングモデルの変革は、従来の計算機利用技術と根本的に異なる技術を要求している。すなわち、従来の逐次計算機やベクトル計算機などの単一プロセッサにおいては、数値アルゴリズム等の研究がフォンノイマン型計算機による処理モデルに基づいており、局所的な処理の流れ及びデータの流れに注目する局所プログラミング技術によって計算機の高効率な利用ができる。一旦単一プロセッサ用の計算技術が開発されれば、普通のソフトウェア技術者がその計算技術を利用し高度な応用ソフトウェアを開発することができた。
しかし、分散メモリ型並列計算機上の並列計算では、局所的プログラミング技術だけでは高い実効性能が得られず、応用ソフトウェア全体を考慮した大域的プログラミング技術が要求される。プログラムの構文的な解析だけでは分散メモリ型並列計算機で高い実効性能を得ることは困難であり、応用ソフトウェアを開発する上で数値アルゴリズムの選択のフェーズ、さらには物理モデル化のフェーズに遡った応用分野の数値シミュレーションの意味を知る必要が生じ、ソフトウェア技術者のレベルでは手に負えない領域となってしまった。
例として、分散メモリ型並列計算機用のFortranプログラムのための並列数値計算ライブラリを利用する場合の問題点を指摘しよう。
数値シミュレーションでは、そこで用いられる数値アルゴリズム及びプログラミング方法によって、計算機での実効性能が大きく左右される。したがって、数値アルゴリズム開発、及びプログラミング方法の研究が重要性を増していった。特定の計算機アーキテクチャ上で極限までその計算性能を引き出すプログラミング能力は、一種の職人芸(匠)である。このため、数値シミュレーションを研究手段としている多くの研究者(ユーザ)は、数値アルゴリズムの開発、あるいは特定の計算機アーキテクチャ上での効率よいプログラミング方法の開発を、数値解析の研究者、数値アルゴリズムの研究者に委ね、ユーザは数値計算ライブラリとして使用することを是としていた。
数値計算ライブラリでは、さまざまな数値アルゴリズムをユーザが簡単に使用できるインタフェースをもつFortranのサブルーチンとしてユーザに提供している。ユーザはサブルーチンを使用する場合、サブルーチンで指定されるデータ構造の規定を守るだけで良く、また必要であれば作業用領域(array)も局所的に確保できる。すなわち、単一プロセッサ上のFortran言語を使った応用ソフトウェアでは、呼び出し側のサブルーチン内で局所的に変数宣言を行うことができ、応用ソフトウェア全体の構造を大幅に変更する必要がない。ユーザ作成の応用ソフトウェアにおけるデータ構造とサブルーチンが指定するデータ構造が異なる場合には、ライブラリを呼び出す直前にデータ構造の入れ替え処理を簡単に追加でき、その修正だけで高い実効性能の数値計算ライブラリが使用可能である。仮にさらに実効性能のよい数値アルゴリズムが開発されたとしてもライブラリとして提供されれば、呼び出し部分を変更するだけで良く、この変更作業は機械的に行うことができる。つまり、ユーザに対して使用上の強い制約を課していなかったと云える。
しかし、分散メモリ型並列計算機上の応用ソフトウェアを開発する場合や単一プロセッサ用の応用ソフトウェアを並列化しようとする場合には、局所的なプログラム構造の把握では性能向上が望めず、プログラム全体を大域的に把握し、データ分割による再配置と並列実行可能な処理の抽出を検討しなければならない。特に、並列数値計算ライブラリを用いる場合、実効性能の高い応用ソフトウェアにするためにはデータ配置が重要なポイントであり、並列数値計算ライブラリのデータ構造と応用ソフトウェアのデータ構造の整合性をとる必要がある。このため、並列数値計算ライブラリを利用する上で、ユーザが作成するプログラムのデータ構造にかなり強い制約が課され、応用ソフトウェアの局所的な変更だけでは対応しきれず、一般のユーザが利用可能な理想的なライブラリにはなり得ない。共有/分散メモリ型並列計算機のようにメモリ階層をもつ計算機を使用する時の応用ソフトウェアのデータ配置問題も深刻である。したがって、一般のユーザが対処できる局所的なプログラム構造の変更では高い実効性能を得ることはできない。
並列計算機の利用技術が進展しないという問題は、「並列計算機をパソコンと同様に誰もが使えるものにしなければならない。」との呪縛から脱却することによって解決できる。すなわち、テラ、ペタフロップス級の超高速並列計算機を用いた大規模並列数値シミュレーションを行うユーザはほんの一握りであり、従来の計算機と同様に一般ユーザが超高速並列計算機を使いこなせる必要はない。超高速並列計算機は、高度な専門性を必要する計算科学のための実験装置であるとの認識を持ち、ユーザによる実験装置の利用では、それを熟知している研究者と共同で大規模数値シミュレーションを行うことが効率的であると思われる。例えば、粒子加速器のような大規模な実験施設を運用しているのは、高度な専門知識を有する研究者と施設を熟知した研究者及び技術者であろう。超高速並列計算機も同様に考えれば気が楽になる。この装置を設置した共同利用施設を作り、物理モデルや数値アルゴリズムレベルで応用ソフトウェアの開発能力をもつ並列応用ソフトウェア研究者をそこに配置し、計算科学研究者との密接な関係の下で優れた応用ソフトウェアを開発できる体制を構築したらどうだろうか。ただし、このような高度な知識が要求されるソフトウェア研究者の仕事を民間のソフトウェア技術者に求めることは困難であり、また社会的需要の少ない計算科学分野のソフトウェア技術者の育成、維持を民間に求めることは得策ではない。
ここでは、大規模な実験装置である超高速並列計算機の開発目的について考えることにしよう。
米国においては、既にASCIプロジェクトにおいて、スーパーコンピュータ開発のための潤沢な国家予算が計算機産業界に投入されている。しかし、このプロジェクトの主目的は、スーパーコンピュータ開発そのものではなく、それを利用した応用分野の課題解決である。1998年2月3日米国ロスアラモス国立研究所におけるクリントン米国大統領のスピーチにおいても、ASCI計画において開発されたスーパーコンピュータは、包括的核実験禁止条約の下での核兵器のシミュレーションに限らず、地球温暖化の影響予測や省力化エンジン等の開発にも利用されるとの認識を示した。このための30Tflopsのスーパーコンピュータを2001年までに517百万ドルを投入して開発することになっており、さらに2004年までに100Tflopsのスーパーコンピュータの開発が計画されている。ここで開発されたプロセッサ技術は、民生品としてすぐに利用可能であることが特徴である。
日本においては、科学技術庁が推進している「地球シミュレータ」計画において、地球変動予測を行うための応用ソフトウェアの開発とともに、ベクトル計算機を要素計算機とした地球環境シミュレーション専用の分散メモリ型並列計算機を平成13年度に完成させることになっており、その要求仕様は実効性能5Tflops以上、主記憶4TB以上としている。この計画の主目的も高速計算機の開発ではなく、地球上の複雑な諸現象に対する大規模かつ高精度な数値シミュレーションによる地球変動の解明にある。たとえば、局所的な気象現象では高分解能モデルが必要であり、その計算のためには現在のスーパーコンピュータの計算能力でも不十分であるため、より高性能な計算機の開発が求められている。この計画の推進により、地球変動に関する理解が飛躍的に進展するものと期待される。
以上の状況のように、科学技術計算のための超高速並列計算機は、既に応用分野に対する専用計算機という位置づけで開発されている。過去、国主導の計算機開発は計算機産業の育成に重点がおかれていたが、今後次世代の超高速並列計算機開発においては、計算機産業の維持、発展のために開発資金を投入するのではなく、ある特定応用分野の計算科学技術を発展させるための専用計算機開発を国主導で実施することが肝要ではないだろうか。その開発過程において半導体製造プロセスの高度化や実装技術の高度化、普及品としてのプロセッサ開発や計算機開発への波及効果が間接的効果として期待される。
超高速計算機が必要な応用分野の選択過程においては、そのニーズに関するさまざまな応用分野の研究者へのヒアリングも必要であるが、むしろ超高速並列計算機を用いた数値シミュレーションが社会に与えるインパクトを評価することが重要である。すなわち、数値シミュレーションによる実質的な開発コスト削減率等について正確に把握すべきである。たとえば、ボーイング社の航空機製造では、開発コストの削減を目的に、設計に必要な大量のパラメータサーベイを数値シミュレーションによって行い、模型を用いた風洞実験に替えることにより大幅なコスト削減を達成したとの事実がある。産業界において数値シミュレーションを適用した場合のコスト削減の具体例を調査し、そのコスト削減分を計算機開発に投入すれば、かなり大規模な超高速並列計算機が開発できるのではないだろうか。今後、超高速並列計算機開発のために大量の国家予算を投入するとすれば、実験代替をした場合の損益分岐点を明確にすべきであろう。もちろん、数値シミュレーションによって得られる成果は、一般大衆に直に反映され利益をもたらす応用分野のものである必要がある。
運用においては、巨額の経費を投入して開発された超高速並列計算機は一極集中の共用実験装置とするべきである。ネットワークコンピューティング技術はここ数年で格段に進歩することが期待され、開発された計算機を分散して設置することも考えられるが、マシンタイムの確保など全体の計算機資源を占有する運用上の調整が困難となり、全体の計算性能を発揮できなくなる可能性があるためである。共同利用施設には並列応用ソフトウェア研究者を配置し、計算科学の研究者と連携を取りながら、大規模な数値シミュレーションを実施する利用体制が望ましい。
超高速並列計算機の開発が可能であるとした時、その実験装置の能力を極限まで引き出すことのできる応用ソフトウェア研究者の確保が次の課題である。
日本には計算機開発に対して高い能力があるのに、優秀なソフトウェア研究者、技術者が輩出しにくく、たまたま優れたソフトウェアが開発されても世界的に普及していない。以下の理由が考えられる。
これらを解決するために省庁間の壁を越えた国としての政策を実施しない限り、日本のソフトウェア技術は育っていかないと思われる。特に、計算科学の並列応用ソフトウェア研究者の育成を怠れば、超高速並列計算機の需要は見い出せないであろう。また、超高速並列計算機が計算科学のための専用計算機として位置付けられても、それを利用できる応用ソフトウェアの開発、維持体制が整備されて行かなければ開発したハードウェアはただの箱になってしまう恐れがある。
応用ソフトウェアを含む計算機ソフトウェアはある種の芸術品である。したがって、その成熟は一朝一夕に達成されるものではなく、ソフトウェア職人(匠)の待遇を改善し、気長に輩出を待つ以外に手はない。計算科学分野に限らず、安易に高度な自動化ソフトウェアを開発することはソフトウェア職人の衰退をもたらし、ソフトウェア技術が消滅してしまう可能性を秘めている。近い将来並列化のプログラミング技術をもつ人間が無形文化財の指定を受けるなどの状況には陥りたくない。特に、計算科学のための応用ソフトウェア研究者、技術者は、高い専門能力を備えている必要があり、その確保、育成に努力すべきである。給与面、福利厚生面での優遇も効果があると思われる。
最後に本稿における提言を、以下のようにまとめておこう。