第3章　ハイエンドコンピューティング研究開発の動向

3.　一様等方性乱流シミュレーション
　地球シミュレータ上で大規模乱流シミュレーションを行うために、フーリエ・スペクトル法に基づく並列直接数値シミュレーション（DNS: Direct Numerical Simulation）コードTrans7を開発し、非圧縮一様等方性乱流の世界最大規模直接数値シミュレーション（計算格子点数4096³）を実現した[5]、[6]。この成果により、2002年米国ボルチモアで開催された国際会議SC2002において、ゴードンベル賞特別賞を受賞することができた。ここでは、コード概要、並列化手法、数値シミュレーション結果の一部について述べる。

3.1　基礎方程式と数値計算法
　3次元立方領域Ω= [0,2π]×[0,2π]×[0,2π]を基本周期領域として、単位密度の非圧縮性流体の運動を考える。流体の運動は外力のある3次元ナビエ・ストークス方程式と連続の式で表される。

SPACE

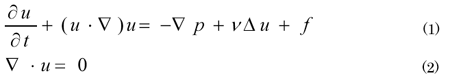ここで、uは速度、pは圧力、νは動粘性係数、fは∇・f=0を満たす外力である。これを渦度形式で表現した方程式を基礎方程式とした。
　このNS方程式を離散化する方法は幾つかあるが、ここではスペクトル法を用いた。スペクトル法は、物理空間の変数を直交関数によって級数展開するものであり、物理空間の変数が十分滑らかであるという条件の下では、項数の増加に対して解が指数的に収束するという性質があり、精度が高く、乱流の振舞いの解析や大気大循環モデルに用いられている方法である。特に、乱流解析では渦のスペクトル成分に関する統計量が重要な物理量となるので、スペクトル法は最適な手法となっている。ここでは、周期境界条件に対応するために3次元フーリエ級数展開を用いた。式（2）及び渦度方程式をフーリエ級数により離散化し、整理すると次の式が得られる。

SPACE

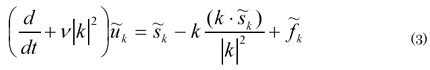　ここで、は−（u×ω）のフーリエ係数である。非線形項の計算には擬スペクトル法が有効である。すなわち、フーリエ空間における畳み込みを計算するために、uのフーリエ係数及びωのフーリエ係数を実空間に変換し、実空間で各格子点（格子点数N³）の外積を求めた後、それのフーリエ係数を求める方法である。この1回の評価のために、3次元フーリエ変換を9回適用しなければならないが、高速フーリエ変換（FFT）を用いれば、非線形項の計算量をO（N⁴）からO（N³logN）にすることができ、フーリエ空間における畳み込み演算（直接和）を行った場合の計算量O（N⁶）と比べるとNが大きい場合には大幅に計算時間の節約が可能である。また、物理空間の値は実変数であるから、実FFTを適用して計算量をさらに減らすことが可能である。
　しかし、擬スペクトル法を用いた非線形項の計算ではエイリアジング誤差が生じるため、畳み込みの正確な値を得るためにはその誤差を除去する必要がある。高波数モードの打ち切りだけでエイリアジング誤差を除去できる3/2則は簡便な方法であり、大気大循環モデルでも用いられているが、畳み込みの正確な値が求まるモード数（有効モード数と呼ぶ）はフーリエ項数N³の（2/3）³になり、3次元実FFTでN³の計算を行う割には十分な解像度が得られない。一方、phase shift 法は、実空間において（1,1,1）方向に半メッシュだけずらした（phase shiftした）格子点でも非線形項の評価を行うことによってエイリアジング誤差を除去する方法である。波数k> √2N/3の高波数モード打ち切りと合わせて完全にエイリアジングエラーが除去可能である。開発したコードではこの方法を用いた。
　また、式（3）の常微分方程式の時間積分には4次精度の4段ルンゲ・クッタ法を用いた。

3.2　並列化手法
　前節の数値計算法に基づく逐次版DNSコードTrans7を開発した。このコードはFortranで書かれており、主要な変数の個数は格子点数N³の25倍である。エネルギースペクトルの最小値と最大値が表現できるように変数はすべて倍精度変数とすると、N=512では約25GBが必要となり、地球シミュレータの一つの計算ノードで実行できない。より大きなNに対するメモリ容量を見積もると、N=4096で約12.5TBになり地球シミュレータ全体でも計算不可能である。このため、格子点数4096³では3次元FFT部分を含む非線形項の計算を倍精度演算、そのほかの部分は単精度演算として実行した。
　コードの並列化では、スペクトル空間のフーリエ係数をk₃方向、物理空間の変数をy方向に分割する領域分割法を用いた。この時、3次元実FFTにおいてz方向に1次元FFTを適用する部分とy方向に1次元FFT を適用する部分の間でデータ転置を行うこととし、MPIライブラリを用いてそれを実現した。データ転置では、全てのMPIプロセス間同士でのデータ交換が必要である。MPIプロセス数をn_mpi とすると、1回の3次元実FFTにおいて、ひとつのMPIプロセスから、他の分割領域の計算を担当する（n_mpi-1）個のうち任意のひとつのMPIプロセスに送られるデータ個数はN³/2（n_mpi）²である。各MPIプロセスは自分以外の転送先に対して、N³/2（n_mpi）²個のデータを（n_mpi-1） 回転送し、（n_mpi-1）個の他のMPIプロセスから送られてくるデータを受けとって、データ転置が完了する。
　また、地球シミュレータのハードウェア性能を十分発揮させるために、地球シミュレータ特有の並列プログラミング技法、すなわちプロセッサ内ベクトル処理、ノード内（共有メモリ）並列処理、ノード間（分散メモリ）並列処理の3レベルの並列処理を考慮したプログラミング技法を適用した。これにより高効率の計算性能が得られる。本コードでは、計算時間の90％以上が3次元高速フーリエ変換（FFT）によって消費されており、この部分の高速化が高い自由度のDNS達成のポイントであった。並列化3次元FFTでは、 3つの空間軸の内、ひとつの軸（例えばz軸）に対し領域分割法によるノード間並列処理を行い、その他の軸（x,y軸）の処理をノード内並列処理とベクトル処理で行った。特に2基底FFTで見られるメモリアクセスのボトルネックを避けるために、ループ内演算数が多くメモリアクセスの少ないベクトル処理可能な4基底FFTを用い、この部分の実効性能をピーク性能の約60％に引き上げた。また、分割方向であるz軸に対するFFTでは、その計算を1つのノード内で実行出来るように、領域分割軸を変更するためのデータ転置を行うが、高速なノード間クロスバスイッチとリモートメモリへの直接アクセス可能なハードウェア（RDMA機構）によって高速に実行することが出来た。

3.3　シミュレーション結果
　Trans7 による計算結果の妥当性を検証するために、Trans7を用いてN=512（格子点数512³）のDNSを行った。速度場の初期条件は、エネルギースペクトルE（k）=a k⁴ exp{-b k²}に従う一様等方的なランダムな速度場で、周期境界条件を満足するように与えた。Δt = 0.001、動粘度ν＝0.000763とし、十分乱流場が発達しエンストロフィー（渦度の2乗平均の1/2）が安定するt=10まで時間発展させた。乱流の統計的準定常状態を得るための外力fとして、低波数領域（|k| < 2.5）に負の粘性を仮定し、その値は全エネルギーが一定に保たれるように各時間ステップで調整した。t=10でのテーラー長λに基づくレイノルズ数は、R_λ≒164であった。この結果、波数領域4 < k < 16近傍において慣性小領域におけるコルモゴロフのエネルギースペクトルが確認された。
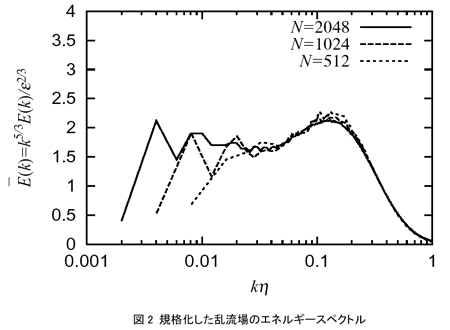
　さらに、格子点数2048³、4096³の世界最大規模の数値シミュレーションを実施した[7]、[8]。図2は規格化した乱流場のエネルギースペクトルである。格子点数2048³のDNSでは、E（k）≒k^-5/3となるコルモゴロフのk^-5/3則がより広い波数領域で確認できる。512台のノードを用いた時の格子点数2048³のDNSの計算時間は、1時間ステップあたり約7秒、約16テラフロップスの高い実効性能（ピーク性能比50%）を達成した。これは地球シミュレータのハードウェア性能を最大限に引き出す注意深い並列プログラミング技法によるところが大きい。格子点数4096³のDNSの1時間ステップの計算時間は約30秒であった。詳細なシミュレーションの結果については、参考文献[6]、[7]をご覧頂きたい。

4.　まとめ
　地球シミュレータハードウェアの性能評価を行うと共に、超大規模な乱流DNSを実現することを目指し、地球シミュレータ用に最適化したDNSコードを開発した。その結果、512ノードを用いた格子点数2048³のDNSにおいて、16.4Tflopsの超高速計算と従来のDNSと比較して桁違いに大規模な格子点数4096³のDNSを実現することが出来た。DNSによって得られた乱流場が、乱流の統計力学の構築など今後の乱流研究において大きな成果が期待される。

参考文献

[1] 後藤,石原,乱流の謎にせまる計算科学,パリティ,Vol.17,No.10,pp.27-33 （2002）

[2] 横川,谷,地球シミュレータ計画, 情報処理, Vol.41, No.4, pp.369-374 （2000）

[3] S. Habata, M. Yokokawa, and S. Kitawaki, “The Earth Simulator System,” NEC Research and Development, Vol.44, No.1, pp.21-26 （2003）

[4] 上原,田村,横川,地球シミュレータの計算ノード上でのMPI性能評価,「計算科学とハイパフォーマンスコンピューティング」シンポジウム（HPCS2002）,pp.73-80 （2002）

[5] 横川,斉藤,石原,金田,地球シミュレータ上の一様等方性乱流シミュレーション,「計算科学とハイパフォーマンスコンピューティング」シンポジウム（HPCS2002）,pp.125-131 （2002）

[6] M. Yokokawa, K. Itakura, A. Uno, T. Ishihara, and Y. Kaneda, “16.4-Tflops Direct Numerical Simulation of Turbulence by a Fourier Spectral Method on the Earth Simulator,” Proc. Of the IEEE/ACM SC2002 Conference （CD-ROM）, Baltimore, November 16-12 （2002）.

[7] Y. Kaneda, T. Ishihara, M. Yokokawa, K. Itakura, and A. Uno, “Energy dissipation rate and energy spectrum in high resolution direct numerical simulations of turbulence in a periodic box,” Physics of Fluids, Vol.15, No.2, L21-L24 （2003）.

[8] 横川,「地球シミュレータ」による世界最大規模乱流シミュレーション,パリティ,Vol.17,No.10,丸善 （2002）

[9] 宇野,板倉,横川,石原,金田,地球シミュレータ上での流体コードのスケーラビリティ評価,情処研報 02-HPC-91,pp.55-60 （2002）