3.研究開発の新しい展開と社会へのインパクト
3.1 金融リスク管理と情報処理技術
3.1.1 はじめに
巨大ヘッジファンドの破綻、高度な数学を駆使した高額なデリバティブ取り引きの実態など、近年の金融問題に関連したニュースの幾つかははからずも「金融工学」という研究分野に脚光をあびせることとなった。日本におけるこの分野を研究対象とする学会のひとつであるJAFEE(The Japanese Association of Financial Econometrics and Engineering)のジャーナル(98年号「リスク管理と金融・証券投資戦略」森棟・刈屋編 東洋経済新報社刊)の巻頭言において、金融工学についての以下のような説明がなされている。「金融工学は、広い意味での金融資産価格の変動を分析対象とし、金融的意思決定の理論・分析手法・実証に関わる学問であり、ファイナンス理論、金融経済論、計量経済学、確率過程論、数理統計学、数理計画法、コンピュータサイエンス等多くの領域にまたがる学際的応用研究領域である。」「欧米では、金融工学は1973年にブラックとショールズが株式オプション理論を展開して以来、派生証券理論、ポートフォリオ理論・分析、アセット・アロケーション、アセット・ライアビリティ・マネジメント(ALM)、金融リスク管理論等を中心として急速に発展した。残念ながら日本の金融工学は、欧米に比べかなり遅れをとっている領域である。」
筆者の現在の専門分野はデータマイニングを中心としたデータ工学であるが、97年、98年をつうじて、IBMの金融リスク管理関連のプロジェクトに参画し、金融工学の一つの重要なテーマである「金融リスク管理」問題にデータ工学の専門家として触れてきた。本報告では、筆者が経験した「金融リスク管理」の一つである信用リスク定量化問題を中心として、情報処理技術、とくにデータマイニング、機械学習技術が、この分野においてどのように応用され、今後どのような貢献が期待されるかを簡単に解説する。金融工学分野においては、情報処理技術の貢献が期待される諸問題がまだ数多く存在し、今後もおおいに発展してゆく可能性が高い点を実感した。また、技術のみならず、制度上の問題点もいくつか存在している。もちろん金融工学と情報処理技術を達観して意見を述べることは、浅学であり、この分野での経験も少ない筆者の能力をはるかに超えているが、本報告では、できうるかぎり広い視点からの現状の分析、将来像、解決すべき問題点について触れている。尚、本報告は「人間主体の知的情報技術調査ワーキンググループ」の主旨に従い、本ワーキンググループの委員として筆者個人が信じるところを述べたものであり、筆者の所属する組織の意見・見解を代表するものではありません。
3.1.2 データマイニング技術を利用したリスク管理事例
本節では、筆者が日本IBMにおいて97年より参加している「信用リスク定量化」に関するプロジェクトで実際にデータマイニング技術を応用した事例を中心に紹介する。このプロジェクトでは98年に「倒産確率算定システムIBMデフォルトメータ」という製品を発表している。また、実際にこの製品やプロジェクトでのノウハウはSIプロジェクトとして、各金融機関、各企業で応用されている。
3.1.2.1 信用リスク定量化問題への取り組み
近年、データベースから属性やデータ間に成り立つ法則(ルール)を発掘し、経営戦略を立案するうえで役に立つ法則をえる「データマイニング」と呼ばれる研究が盛んに行なわれ、その成果はあらゆる業界のデータ分析に応用されている。特に金融業界は、データ分析能力を、経営の死命を決することもある重要な技術として認識し、古くから多変量解析、シュミレーションなど様々なデータ分析技術を応用してきた。近年はデータマイニングも盛んに行われている。
管理したい、あるいは、分析したい金融リスクの一つに「信用リスク」と呼ばれるものがある。信用リスクとは「倒産」の危険性のことを示し、金融機関はいうまでもなく、あらゆる会社の財務部門や審査部門においては、取引先の倒産の危険性がどの程度あるのか知ることは、非常に重要かつ困難な課題である。
そんな課題に対する一つの取り組みとして、我々は、企業の財務データと債務の履行状況を含むデータベースから学習した決定木を利用し、企業の信用リスクを定量化するこころみを行なった。財務データのような数値中心のデータベースから知識をマイニングする場合、データ間の相関関係を考慮しなければならない。我々は決定木の判別ルールとして領域ルールを利用することで、この問題に対処した。
領域ルールは2次元、つまり2変量のデータ間に対する相関にしか対処していないが、ルールを視覚的に表現できデータ間の相関を理解しやすい。また、3変量以上を利用する従来の多変量解析の各手法に比べ計算時間が非常に短いといった利点がある。予測精度の面においても、実在する金融データによる実験で検証してみたところ、3変量以上を利用する線形およびロジット回帰モデルを使った多変量解析の手法や、ニューラルネットワークなどと比較して、ほぼ同等の結果を得ることができた。このような結果から、領域ルールを利用するデータマイニング手法は金融関連データのような数値属性中心のデータベースに対する分析手法として期待できる。
3.1.2.2 金融データにおける属性間の相関
金融業界で扱うデータの多くは財務諸表上の勘定科目などのような連続数値型データである。従って、金融業界で扱うデータベースには、属性の多くが連続数値型である、属性の数が多いといった特徴がある。多くの数値属性を持つデータベースでは数値間の相関関係を考慮する必要があり、金融データベースもその例外ではない。実際に、金融の分野では、そのデータ分析手法として、様々な多変量解析の手法が使われることが多い。それは、この分野で扱うデータ分析では、相関関係に対処する必要が強かったことを示している。
金融業界においても、データベースに潜む重要な法則を発見するデータマイニング技術に対する要求は高く、徐々に、データマイニングの応用事例も増え始めている。しかしながら、従来のデータマイニング技術では、多次元の数値データベースを扱う場合、数値間の相関関係にうまく対処できないといった問題があった。
例として、企業の財務データについて考える。企業の財務体質の善し悪しを測る、重要な比率の一つに、以下のように定義される“return on assets”(ROA)と呼ばれる比率がある。
Operating Earnings |
||
| ROA= | ――――――――― | ×100% |
Net Operating Assets |
この比率の高い企業は財務体質上、良好な企業と判断される。この重要な比率は、企業の“Net Operating Assets”、および、“Operating Earnings”という二つの財務データ属性の比から求まるもので、この例からも財務分析には、複数の属性間の相関や比率などが欠かせないことがわかる。
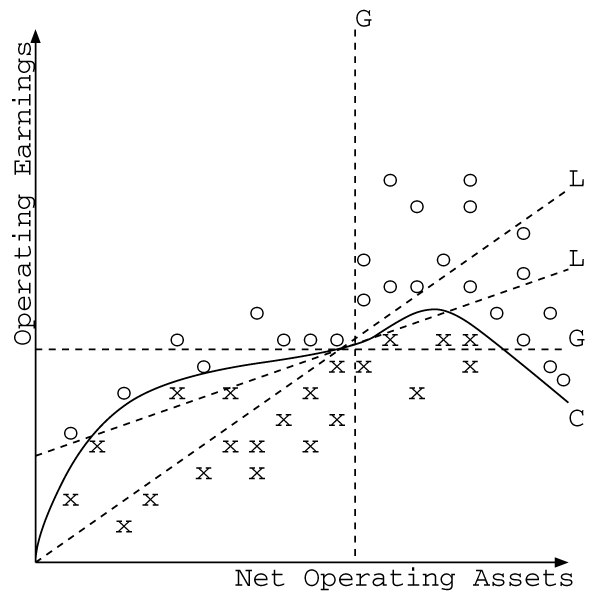
今、図3.1-1に、上述の2つの財務データ属性と債務不履行を起こした企業、起こさなかった企業の関係を示す。図中のX軸は“Net Operating Assets”をY軸が“Operating Earnings”を示し、この2次元平面上に債務不履行をおこさなかった企業を“o”として、債務不履行を起こした企業を“x”としてプロットした。

図3.1-1 Rules for Correlated Data
債務不履行に関する分析を行ないたい場合、図中の○と×を、よりはっきりと分離する判別ルールがよいルールと考えられる。従来のデータマイニングシステムの多くは、ルールを求める際に、単一の数値データを使った図中のGで示されるような軸に平行な直線で表わされるような、ギロチンカットルールでデータを判別する。しかし、軸に平行な直線、あるいは長方形による判別では、図中の○と×をうまく分離することができない。
図中のLで示されるルールは線形相関を仮定した多変量解析の手法や、マルチバリエートテストと呼ばれるΣ
iaiAi < c (ここでai (i = 1,..,n)およびcは定数、Aiはある属性Aiの値を示す変数)のような式で表わされる線形ルールを利用できる一部のデータマイニングシステムで得られるものである。変数の相関関係が線形であった場合、これらの線形回帰的手法で充分よい判別ルールを得ることができる。しかし、実データに存在している相関のパターンにはあらゆる非線型の形が存在し、この手法で対処できるケースは限られている。尚、上述の各企業のROAは、この平面上の原点と企業の点を結ぶ直線の傾きそのものである。この比率の重要性は広く認知され、かつ、いろいろな場面で利用されるため、企業情報のデータベースの一属性としてにあらかじめ登録されているケースも多い。その場合、従来のギロチンカットでLに相当する判別性能を得ることも可能になるが、それはあらかじめ、重要な比率、つまり、ある注目する属性間の相関が、広く認知され、かつ、線形である場合に限られた場合であり、未知のルールを発見することに重点をおくデータマイニングへの要求を満たすことはない。
このデータに見られるように、企業の債務の履行状況の健全度は、“Net Operating Assets”、“Operating Earnings”の二つの属性の比率により、かなり、よく評価できるが、実際は、企業の“Net Operating Assets”の規模に応じて、その適切な比率は異なっている。つまり、図中のCのような、非線型の相関ルールを発見することが、財務分析上必要となっている。
3.1.2.3 領域ルールによる非線型相関の発見
データ間の相関に対処するための手法としては、線形回帰、ロジスティック回帰などの手法が使われることが多い。これらは、多変量にまたがる相関を、関数として表現できる反面、上述のように対応可能な相関の形式か限られている。また、カーネル密度関数などの非線型モデルはあらゆる相関に対処は可能ではあるが、多変量になった場合、関数で表わされたルールの意味を直感的に把握するのが難しくなってしまう。この場合、変数を絞りこめば、わかりやすいルールとなるが、多変量から2、3変量程度に絞り込む組み合わせは、膨大な数に登るため時間、空間両面のパフォーマンス面での問題も大きい。
我々の研究グループでは、数値データを使ったマイニング技術に焦点をおいた研究を進めておりその一つの成果として、2変量にまたがるルールとして、領域ルールの高速計算手法を開発している。そこで、判別ルールとして領域ルールを用いることで、2変量に対するあらゆる相関に対処した。この手法は、理解しやすく、かつ、高速に計算可能である。この手法自体は、2変量以上の場合にも拡張可能であるが、その場合に増加する計算コスト、ルールの理解しやすさの問題、精度を維持するためのデータ量の確保が難しくなるなどの問題点を考慮し、現在は、2変量に限定して適用している。実際、実データを用いて実験してみたところ2変量でも、かなりよい成果が得られている。
2変量に対応する領域を考える場合、まず、2変量に対応する2次元平面を構成し、その平面を、ほぼデータ数が等しくなるよう各軸を離散化し、ピクセルグリッド化する。我々は、このように作られたグリッド上で最適なピクセルグリッド領域を計算する。しかし、任意の形の連続ピクセル領域の最適化はNP困難な問題として分類されるため、我々は領域の形にある程度の制約を持たせている。ただしその制約はあまり領域の表現力を損なうものではない。
企業の財務データでは属性の数が70以上にもおよぶ。これらの属性の中から領域を構成する平面を考える場合、約2500とおり組み合わせが対象となる。どの平面が分析上重要であるかは、前もってわからないため、これらをすべて調べる必要がある。
以下の表は、自動生成したピクセルグリッドデータ上で、最適なx-monotone領域(縦方向に連続)およびrectilinear convex領域(縦横方向に連続)を求るのに要した計算時間(秒)を示す。実験は66MHzのPOWER2チップと256MBのメインメモリをもつIBM RS/6000ワークステーション上のAIX4.1オペレーティングシステム環境上での実行時間を計測したものである。このように高速なアルゴリズムが開発されたために、多変量の財務データであっても、領域を利用したデータマイニングが可能となった。財務データに限らず金融関連のデータには多変量であるものが多いため、この手法は金融データ分析のあらゆる側面で応用することができる。
―――――――――――――――――― X-monotone
Rectilinear
―――――――――――――――――― #pixel time time ―――――――――――――――――― 102
0.05
0.07 202
0.22
0.64
302
0.50
2.30
402
0.83
5.41
502
1.60
11.0
――――――――――――――――――
3.1.2.4 財務データ分析の例
以下の表は1992年から1996年までの日本企業の財務内容を表わすデータベースである。このデータベースには“
ID” (ID of a company), “Net Income / Sales,” “Equity Ratio”など69種類の数値属性と、その企業の債務の履行状況を示す“Default”という属性がある。債務履行状況を特徴づける判別ルールを求めるため、債務不履行を起こした“Default”属性値が“D”で示される1036件の企業データと、起こさなかった“N”で示される1036件の企業データを使い決定木を作成した。
――――――――――――――――――――――――――――――――――――― ID Net Income / Sales (%) Equity Ratio (%) ...
Default ――――――――――――――――――――――――――――――――――――― xxx
5.119
25.876
...
N
xxx.
1.248.
3.847.
....
N
xxx.
0.355.
8.941.
....
D
xxx.
1.235.
38.886.
....
N
....
....
....
....
...
xxx.
-0.096.
4.111.
...
D
―――――――――――――――――――――――――――――――――――――
図3.1-2はこのデータベースから発見された債務の履行状況を財務状態から判定するための最も重要な領域ルールを示す。69個の数値属性からなる平面の取り方には2300通り以上の組み合わせがあるが、我々はこれらのすべての平面上で最適な領域を計算し、その中で最適なものを探し出した。我々の利用する高速な領域算出アルゴリズムは、このような多次元データベースに対しても十分適応可能であった。図の領域は横軸を“EBIT / Sales”縦軸を“Equity Ratio”とし、全企業の集合“S”領域内の集合“S1”と領域外の集合“S2”とに以下のように分割している。
| ――――――――――――――――――――――――――――――――――――― | |||
| No. of companies | No. of default | No. of non-default | |
| ――――――――――――――――――――――――――――――――――――― | |||
| S: All data | 2072 | 1036 | 1036 |
| S1: Inside | 969 | 797 | 172 |
| S2: Outside | 1103 | 239 | 864 |
| ――――――――――――――――――――――――――――――――――――― | |||
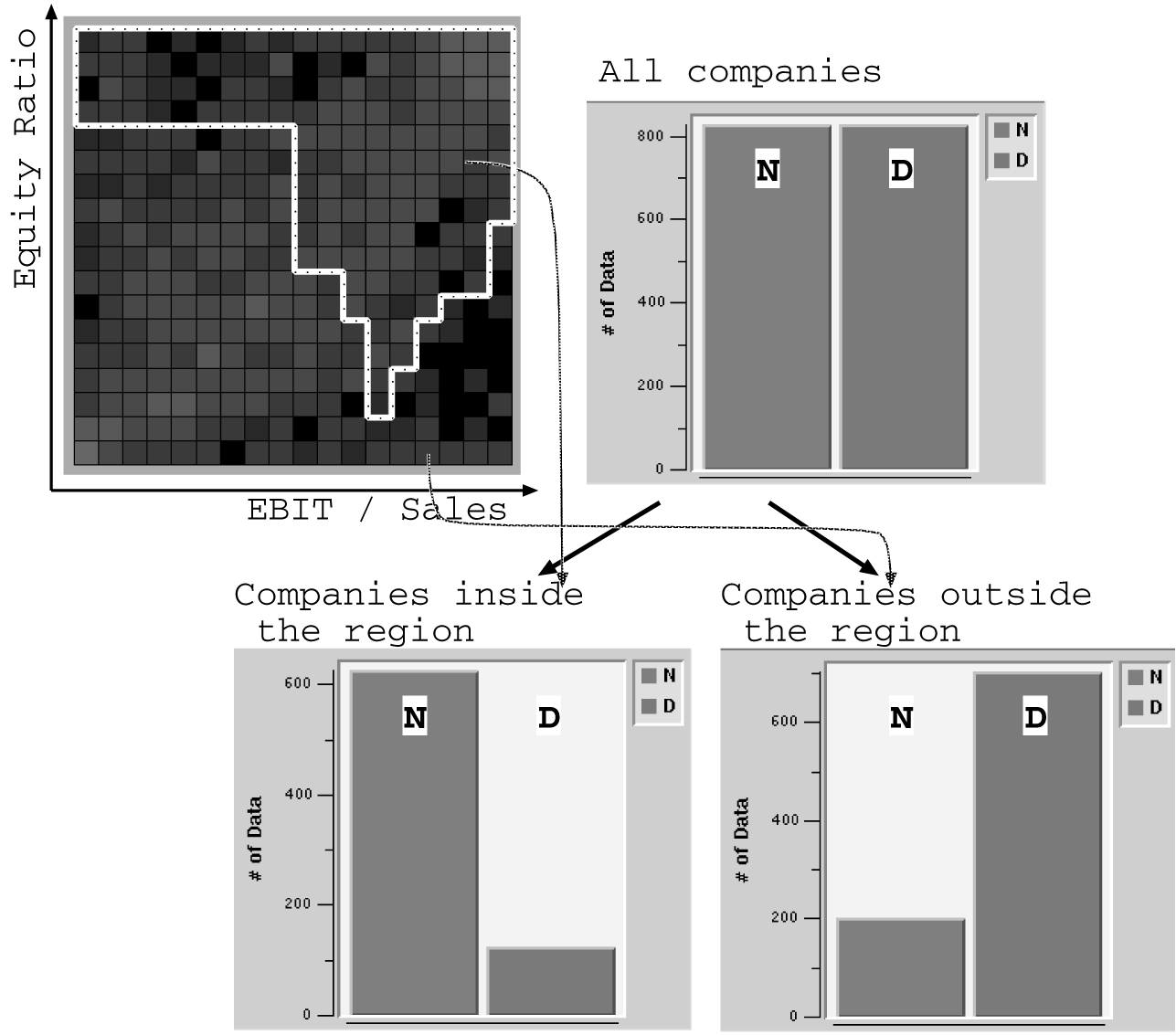
図3.1-2 Rules for Analyzing Credit Risk
このような領域ルールをつかって企業の分類を繰り返し、図3.1-3のような決定木を作成した。図中の四角のノードは決定木の終端ノードであることを示し、終端ノードに属する企業のグループでは“N”と“D”の比率が充分に偏っている。このような決定木を使って、企業の財務内容から信用リスクを判定することが可能となる。実際のシステムでは、景気の状態なども加味し、個々の企業の財務内容から見た倒産確率は何%であるかを出力するが、その信用リスク定量化の具体的な手法についての詳述は本報告では省略する。
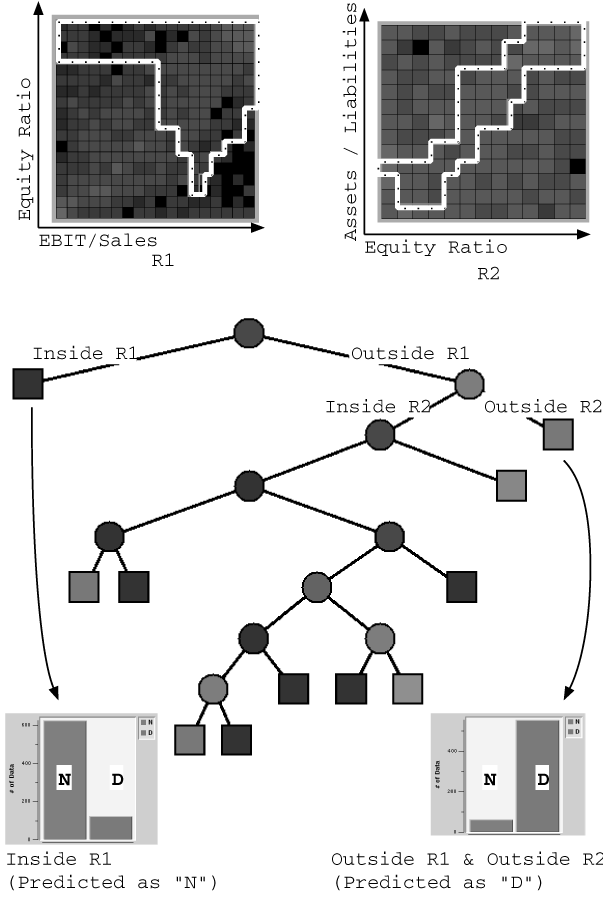
図3.1-3 Decision Tree for Analyzing Credit Risk
3.1.2.5 市場データ分析の例
債務不履行を起こすか、起こさないかといった、範疇型の目的属性の判別ルール以外にも、金利、株価の変動などを目的属性としたルールに対する要求も高い。この場合、後述の市場リスク、スプレッドリスクに関連した問題への応用にもつながる。
以下の表は金、国債、各国通過の対ドルの相場値と、そのときのSP500の値をデータベース化したものである。データベースはNY市場における、1985年最終週から1993年最初の週までの毎月曜における“
BPS”(British poundsterling, i.e., US$/pound),“GDM” (deutschmark, i.e.,US$/mark), “YEN”(Japanese yen, i.e., US$/yen),“TB3M”(3-month Treasury bill yields), “TB30Y” (30-yearsTreasury bill yields),“GOLD”(US$/ounce)の各相場値と、“SP500” (Standard and Poors index)のインデックス値を記録した384件のデータからなる。このデータベースから“SP500”インデックス値に影響を与える重要なルールを見つける。
| ―――――――――――――――――――――――――――― | ||||||
| BPS | GDM | YEN | TB3M | ... | GOLD | SP500 |
| ―――――――――――――――――――――――――――― | ||||||
| 1.443 | .4074 | 00498 | 7.02 | ... | 326.00 | 210.88 |
| 1.446 | .4080 | .00495 | 7.04 | ... | 339.45 | 205.96 |
| 1.437 | .4048 | .00494 | 7.13 | ... | 357.25 | 208.43 |
| 1.404 | .4087 | .00498 | 7.17 | ... | 355.25 | 206.43 |
| ... | ... | ... | ... | ... | ... | ... |
| 1.568 | .6338 | .00907 | 2.91 | 357.50 | 442.31 | |
| ―――――――――――――――――――――――――――― | ||||||
図3.1-4は、このデータベースから発見された“SP500”の値に影響を及ぼす最も重要な領域ルールを示す。図の領域は横軸を“GDM”縦軸を“GOLD”とし、全データ集合“S”を領域内の集合“S1”と領域外の集合“S2”とに以下のように分割している。
| ―――――――――――――――――――――――――――――――― | |||
| No. of data | SP500 mean | SP500 variance | |
| ―――――――――――――――――――――――――――――――― | |||
All Data S |
384 |
324 |
4431 |
Inside Region S1 |
157 |
391 |
1118 |
Outside Region S2 |
227 |
278 |
1489 |
| ―――――――――――――――――――――――――――――――― | |||
このような領域ルールをつかって市場データの分類を繰り返し、図3.1-5のようなリグレッション木を作成した。決定木同様、図中の四角のノードはリグレッション木の終端ノードを示し、終端ノードに属するデータ集合では“SP500”の値の分散がかなり小さく、市場の状況に基づく“SP500”の値を予測することが可能となる。
例にあげた両データともに、実際に線形ではない形の領域ルールが最適なルールとして算出されている点が興味深い。
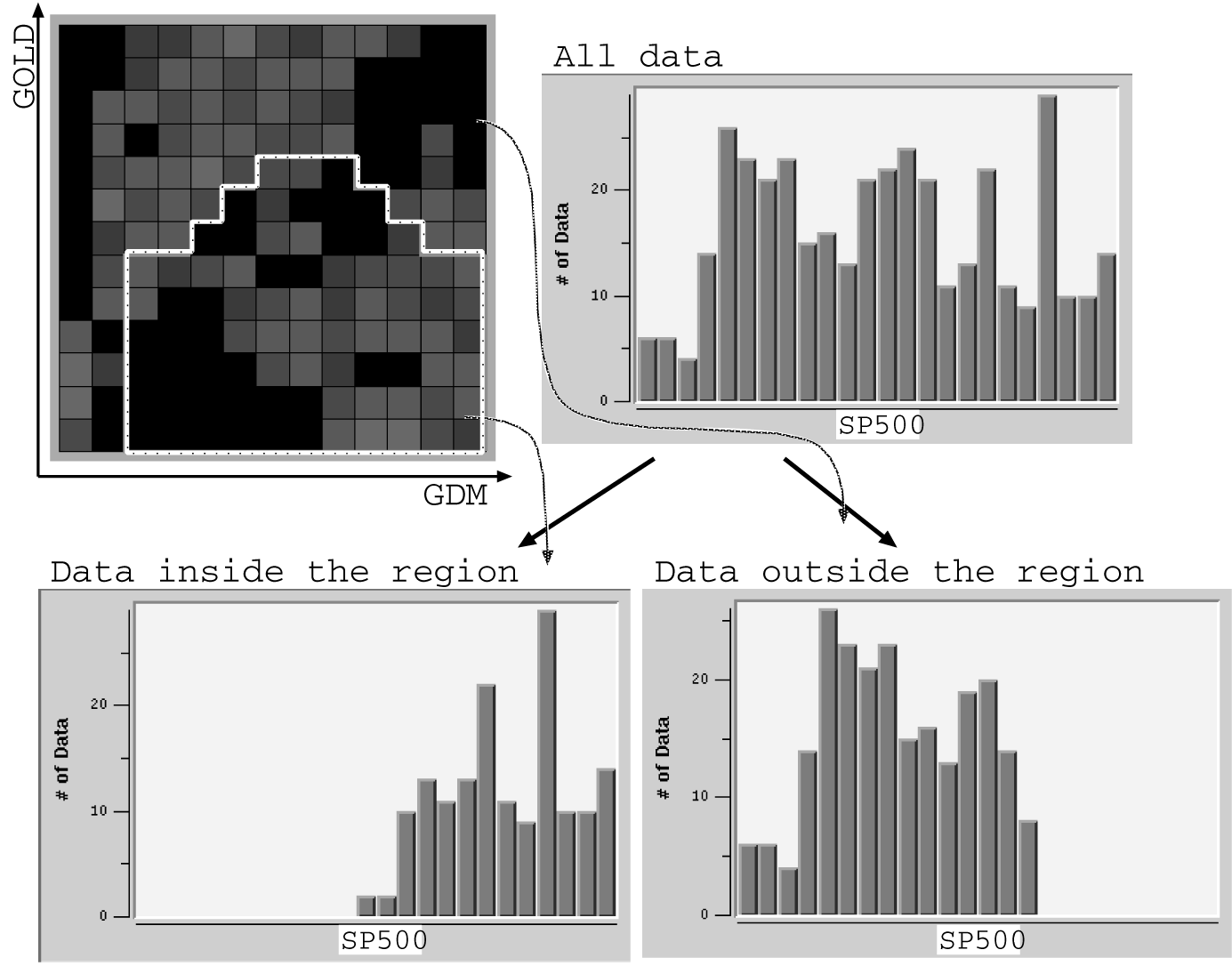
図3.1-4 Rules for Analyzing the Market
3.1.3 金融リスク管理とITビジネスの展望
将来の経済事象を考える時、それらのすべてにはなんらかの不確実性が存在している。例えば、現在保有している証券や貨幣などの金融資産は、市場における価格変動や、為替の変動にともない、その将来における価値を変えていくという不確実性をおびている。そうした不確実性を把握し、管理していく手法として、さまざまな金融リスク管理理論が提唱されている。
金融リスクは大別すると、信用リスクと市場リスクに分けられる。信用リスクは、前述のとおり、取引相手が義務をはたさないことから生じるリスクである。市場リスクは、売買に伴う価格リスク、市場金利の変動に伴う金利リスク、外国為替相場の為替変動に伴う為替リスクなどを総称したものである。金融リスク管理はこうしたリスクを正確に定量化し、自分のもつ資産、債務、偶発債務、デリバティブ取引の定量化されたリスクに応じて、適切な対策を考えることを目的としている。
3.1.3.1 信用リスク
信用リスク管理のためには、まず、取引相手の債務あるいは契約義務不履行の確率の正確な定量化、さらには、取引相手の被る市場リスクの定量化が不可欠である。そうした信用リスク定量化のためには取引相手の財務状態を把握し、それを正確に分析する技術が必要となる。
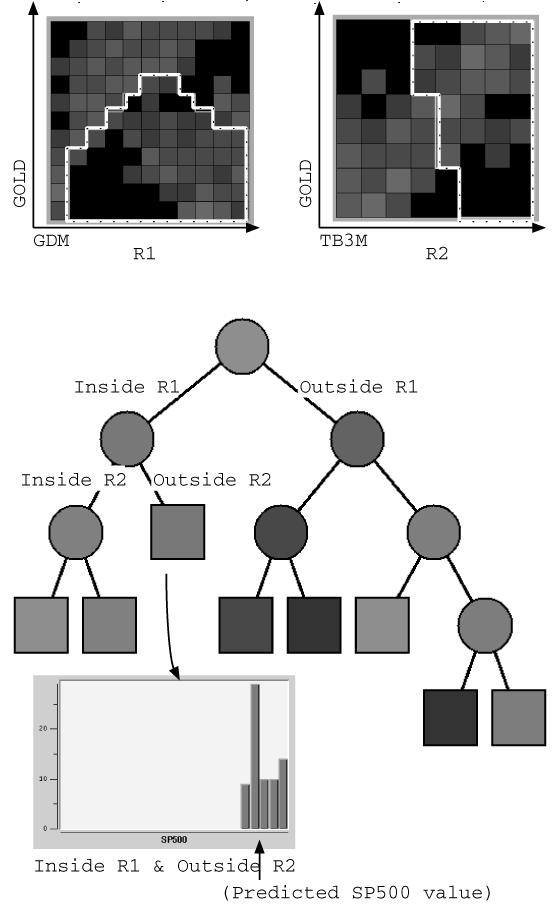
図3.1-5 Regression Tree for Analyzing the Market
制度の面から見た場合、各企業は事業年度ごとに「貸借対照表」「損益計算書」などの財務諸表を商法・証券取引法などに従った様式で作成しなければならない。こうした情報は、投資家や、取引先に正しい情報を与える上で非常に重要な物である。ところが、現行の会計原則では、原資産(債権、株式、通貨、商品)に関する取引はオンバランス取引として貸借対照表に記載される一方、デリバティブ取引はオフバランス取引とよばれ、取引発生時に簿記による取引記載義務がない。デリバティブ以外にも、契約債務、偶発債務などのオフバランス取引が存在し、こうした情報の正確な把握なしには、正確な信用リスクの定量化は難しいと思われる。
一方、技術面から見た場合、我々はデータマイニング技術を駆使し、決定木を利用した判別を行なうというアプローチをとったが、他にも、カーネル密度関数などの多変量判別分析、ニューラルネットワーク、ジェネティックアルゴリズムなどを利用したアプローチも有効であると思われる。しかしながら、信用リスクに影響をおよぼす要因としてはバランスシート上のデータのみならず、為替などのマクロ要因もあり、実際はそれらが複雑に関連している。そうした、複雑な状況を正確に分析するには、さらなる研究が必要である。
3.1.3.2 市場リスク
市場リスク管理のためには、さまざまな金融資産やデリバティブについての、現在における正確な理論価値、および、将来における価値変動の予測が必要となる。
近年では、原資産のみならず、資産から派生した金融派生商品であるデリバティブの取引が盛んに行なわれている。後藤著「デリバティブ時価会計入門」中の資料によると、96年3月末現在で日本のデリバティブ取引の想定元本の規模は大手銀行分だけで1235兆円に達し、国民総生産の2.5倍、東京証券取引所株式時価総額の3.5倍となっている。同著に掲載されているBIS(国際決済銀行)95年12月発表の資料では、デリバティブ想定元本は世界合計で57兆ドル(うち日本の合計13兆ドル)、デリバティブ一日取引高は世界合計で1兆9730億ドル(うち日本合計5893億ドル)となっている(いずれも95年3月末のデータ)。
デリバティブには先物、スワップ、オプションがある。先物は「ある金融資産を、将来のある時点で決済する条件で、その価格と数量を現時点で約定する」取引で、小麦、大豆など商品を対象としたもの(商品先物)と、通貨、株式、株価指数など金融資産を対象としたもの(金融先物)がある。スワップは「取引の当事者双方が、それぞれ相手のもつ債務の履行義務を負う」交換取引のことをいう。たとえば、ある通貨の債務を別のある通貨の債務と交換する通貨スワップ、固定金利と変動金利などの金利の支払債務だけを交換する金利スワップなどがある。オプションはある期日(ヨーロピアン)または、ある期間内(アメリカン)に、あらかじめ決められた価格で金融資産を買う権利(コール)または、売る権利(プット)の取引ことをいう。
これらの取引は、本来は原資産のもつ市場リスクの回避手段として利用される。例えば、ある金融資産を将来に売る予定があるとする。売る時点での価格は市場リスクをもち、その価値は(ときには大きく)変動する。このようなケースでわずかな額のプットオプションの権利金(オプションプレミアム)を支払って、将来、ある価格で売る権利を購入しておけば、その決められた価格以上で、資産を売ることができ、価値下落のリスクを回避できる。また、現在の時点で先物取引の約定を交わしておくという手段も考えられる。他方、こうしたデリバティブを利ざやをかせぐ手段としている投機家、投機家集団もいる。このような投機家は市場を活性化させる一方で、近年はそのような投機家の市場での行動を問題視する意見も多い。
市場リスク管理の必要性からデリバティブの理論価値・時価評価の手法が研究されている。とくにオプション価値の定量化理論は高度な数学知識を必要とする。理論面での研究以外でも、こうした時価評価には大規模な計算機シュミレーションが必要となるため、この分野の技術の発展も多いに期待されている。
3.1.3.3 リスク管理体制
リスク管理技術は理論面やシステム面でこれまでおおいなる発展をしているが、ノーベル経済学賞受賞者など金融界のそうそうたるメンバーを擁するLTCMが破綻の危機に瀕したように、リスク管理はまだ充分ではなく、より複雑な経済事象を広く、深く、正確に把握し、適切に対処していく形で発展していかなければならないと思われる。それとともに、より正確な情報開示と、金融システム安定化のための必要な規制の整備がともなわなければならないと感じる。
デリバティブの発展と、市場のグローバル化にともない、ひとつの企業、銀行、ファンドなどのリスク管理の不備は、世界的な金融危機(システミックリスクの危機)をもたらす可能性をもつ。そのため金融リスクの管理は世界的な重要事項となっている。こうしたリスク管理体制には国際的銀行システムの健全化・安定化のためBIS規制や、G30というグループがまとめたデリバティブ取引のリスク管理への提言などがある。しかしながら、市場のグローバル化がすすんでいる今日では、制度としてのリスク管理体制は、日本に限らず、充分で有効であるとはいいがたい。
現在のところ、裕福で少数の限定された顧客の資産を運用するヘッジファンドは、金融当局の規制をあまりうけていない。この問題点は昨今のヘッジファンド危機のニュースとともに話題にのぼっている。
3.1.4 むすび:「虎穴に入らずんば虎子を得ず」
金融ビックバンにともなって、個人レベルの資産運用においてもブルベア型投資信託など数多くのハイリスク金融商品がおおく出回るようになってきた。こうしたリスク商品では、もちろん元本は保証されず、運用にともなうリスクはあくまで自己責任である。自己責任である以上は個人レベルで、そのリスクをきちんと把握しておく必要がある。しかしながら、個人レベルで運用先のリスクを分析し、納得の上で投資をおこなうために必要な情報が現状では少ないと思われる。
現在、株式上場企業に開示が義務づけられている財務諸表でさえ、実際には粉飾されていたものもいくつか散見されていたように、数少ないリスクを定量化するのに必要な情報もあまり信頼できる物とはいいきれない。実際に我々の開発したデフォルトメータで予測できなかった倒産事例の中には、後日、粉飾決算が発覚したようなケースも存在したとのことである。投資家に対する正確な情報開示の制度の整備・確立が強く望まれる。
今後、リスク商品に投資する一般投資家は増加し、その市場規模も大きくなることが、予測されるが、一般投資家の多くは、金融の専門知識をもたない。そうした一般投資家のニーズに合わせて、開示されている分析可能なデータを分析するためのソフトウエア、投資コンサルティングビジネス、わかりやすい投資関連の情報誌などの関連ビジネスも成長して行くと思われる。情報開示の基盤作り、適切な一般投資家保護のための規制づくりなどでは関連当局のイニシアティブを期待する。
<参考文献>
森棟公夫,刈屋武昭編:「ジャフィージャーナル1998:リスク管理と金融・証券投資戦略」,東洋経済新報社,1998.
森平爽一郎:「倒産確率の推定と信用リスク管理:展望」,In 森棟,刈屋編ジャフィージャーナル1998,pp.3-35, 東洋経済新報社,1998.
呉文二,島村高嘉:「金融読本」(第22版),東洋経済新報社, 1998.
後藤公彦:「デリバティブ時価会計入門−投資決定とリスク管理」,日科技連,1997.
二宮祥一,田島玲,水田秀行:「金融リスク管理におけるIT最前線」,情報処理, vol.39, no.8, 1998.
Fukuda, T., Morimoto, Y., Morishita, S., and Tokuyama, T.:“Data Mining Using Two-Dimensional Optimized Association Rules:Scheme, Algorithms, and Visualization,” In Proceedings of the ACM SIGMOD Conference on Management of Data, pp.13-23, 1996.
Fukuda, T., Morimoto, Y., Morishita, S., and Tokuyama, T.:“Mining Optimized Association Rules for Numeric Attributes,” In Proceedings of the Fifteenth ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems, pp.182-191, 1996.
Morimoto, Y., Fukuda, T., Morishita, S., and Tokuyama, T.:“Implementation and Evaluation of Decision Trees with Range and Region Splitting,”Constraint 2(3/4): pp.401-427, 1997.
Morimoto, Y., Ishii, H., and Morishita, S.: “Efficient Construction of Regression Trees with Range and Region Splittng,” In Proceedings of the 23nd VLDB Conference, pp.166-175, 1997.